Question

【题目】（本小题满分13分）

已知函数，其中．

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）证明： 在区间上恰有个零点．

Answer 1

【答案】（1）（2）详见解析

【解析】试题分析：（Ⅰ）当时， ，求出的值可得切点坐标，求出的值可得切线斜率，由点斜式可得曲线在点处的切线方程；（Ⅱ）求出导函数．由 ，得 ．根据零点存在定理可得存在唯一的， 使得 ， 在区间上单调递增，在区间上单调递减．可证明，从而可得结论.

试题解析：（Ⅰ）当时， ，

所以 ．

因为 ， ，

所以曲线在点处的切线方程为．

（Ⅱ）．

由 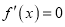，得 ．

因为 ，所以．

当 时， 由 ， 得 ．

所以 存在唯一的， 使得 ．

与在区间上的情况如下：

	↗	极大值	↘

所以 在区间上单调递增，在区间上单调递减．

因为 ，

且 ，

所以 在区间上恰有2个零点．

【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与极值，属于难题.求曲线切线方程的一般步骤是：（1）求出在处的导数，即在点 出的切线斜率（当曲线在处的切线与轴平行时，在 处导数不存在，切线方程为）；（2）由点斜式求得切线方程.