题目内容
8.已知函数f(x)=ax3+bx2(a≠0),在x=1时取得极值3,求:(1)f(x)的表达式;
(2)f(x)的单调区间.
分析 (1)求出函数的导数,根据f(x)在x=1时取得极值3,得到关于a,b的不等式组,解出即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可.
解答 解:(1)f′(x)=3ax2+2bx,
∵f(x)在x=1时取得极值3,
∴$\left\{\begin{array}{l}{f′(1)=3a+2b=0}\\{f(1)=a+b=3}\end{array}\right.$,
解得:a=-6,b=9,
故f(x)=-6x3+9x2;
(2)由(1)得:f′(x)=-18x2+18x=-18x(x-1),
令f′(x)>0,解得:0<x<1,
令f′(x)<0,解得:x>1或x<0,
∴f(x)在(-∞,0),(1,+∞)单调减;[0,1]单调增.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
19.已知函数y=Asin(ωx+φ)(A>0,ω>0)的最大值为4,最小值为-4,最小正周期为$\frac{π}{2}$,直线x=$\frac{π}{3}$是其图象的一条对称轴,则符合条件的函数解析式是( )
| A. | y=4sin(4x+$\frac{π}{6}$) | B. | y=4sin(4x+$\frac{π}{3}$) | C. | y=2sin(4x+$\frac{π}{3}$) | D. | y=2sin(4x+$\frac{π}{6}$) |
3.集合A={x||x|≤2},集合B={x|x<a},如果A∩B=∅,那么a的范围是( )
| A. | a=2 | B. | a≤2 | C. | a=--2 | D. | a≤--2 |
13.在△ABC中,三个角满足2A=B+C,且最大边与最小边分别是方程x2-12x+32=0的两根,则△ABC外接圆的面积为( )
| A. | 16π | B. | 64π | C. | 124π | D. | 156π |
11.若a,b在区间$[{0,\sqrt{3}}]$上取值,则函数$f(x)=\frac{1}{3}a{x^3}+b{x^2}+\frac{1}{4}ax$在R上有两个相异极值点的概率是( )
| A. | $\frac{1}{4}$ | B. | $1-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
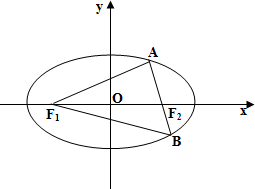 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.