题目内容
对于函数f（x）=sin2（x+
）-cos2（x+
），下列选项中正确的是（ ）
| π |
| 4 |
| π |
| 4 |
A、f（x）在（
| ||||
| B、f（x）的图象关于原点对称 | ||||
| C、f（x）的最小正周期为2π | ||||
| D、f（x）的最大值为2 |
考点：二倍角的余弦,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：直接利用二倍角公式化简，然后利用函数的性质判断选项即可．
解答：
解：函数f（x）=sin2（x+
）-cos2（x+
）=-cos（2x+
）=sin2x．
函数y=sin2x是奇函数，f（x）的图象关于原点对称，B正确．
故选：B．
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
函数y=sin2x是奇函数，f（x）的图象关于原点对称，B正确．
故选：B．
点评：本题考查二倍角公式的应用，正弦函数的基本性质的应用，考查基本知识的熟练程度．
练习册系列答案
相关题目
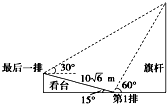某校运动会开幕式上举行升旗仪式，在坡度为15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10| 6 |
| A、10 m | ||
| B、30 m | ||
C、10
| ||
D、10
|
已知函数f（x）=ln|x|+x2，则下列各式一定成立的是（ ）
| A、f（-7）＜f（6） |
| B、f（-3）＞f（2） |
| C、f（-1）＞f（3） |
| D、f（-e）＜f（-2） |
下列给出的赋值语句中正确的是（ ）
| A、3=A | B、x=-x |
| C、B=A=2 | D、x+y=0 |
设a=
，b=
，则a+b=（ ）
| 3 | (-8)3 |
| (-10)2 |
| A、-18 | B、18 | C、-2 | D、2 |
若0＜x＜y＜1，则（ ）
| A、3y＜3x | ||||
B、(
| ||||
| C、logx3＜logy3 | ||||
D、x-
|
已知抛物线x2=y+1上一定点A（-1，0）和两动点P、Q，当PA⊥PQ时，点Q的横坐标的取值范围（ ）
| A、（-∞，-3]∪[1，+∞） |
| B、[1，+∞） |
| C、[-3，-1] |
| D、（-∞，-3] |
复数Z=
，则复数
对应的点在（ ）
| ||
1-
|
. |
| Z |
| A、第一象限或第三象限 |
| B、y轴负半轴上 |
| C、x轴正半轴上 |
| D、第二象限或第四象限 |