题目内容
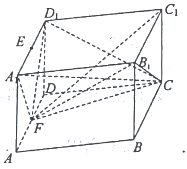
【题目】如图,三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,根据三角形中位线得到
,根据三角形中位线得到![]() ,进而得到线面平行;(2)根据二面角的定义可证得
,进而得到线面平行;(2)根据二面角的定义可证得![]() 是二面角
是二面角![]() 的平面角,在三角形BD
的平面角,在三角形BD![]() 中求解即可。
中求解即可。
解析:
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
因为![]() 是三棱柱,所有四边形
是三棱柱,所有四边形![]() 为平行四边形.
为平行四边形.
所以![]() 是
是![]() 的中点.
的中点.
因为点![]() 是
是![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,
的中位线,
所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.

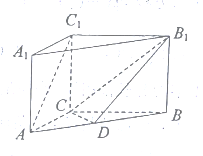
(2)![]() 是二面角
是二面角![]() 的平面角.
的平面角.
事实上,因为![]() 面
面![]() ,
, ![]() 面
面![]() ,所以
,所以![]() .
.
在![]() 中,
中, ![]() ,
, ![]() 是底边
是底边![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在直角三角形 ![]() 中,
中, ![]() ,
, ![]() ,
,
所以 ![]() 为等腰直角三角形,
为等腰直角三角形,
所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.