题目内容
【题目】已知函数
对任意实数
均有
，其中常数
为负数，且
在区间
上有表达式
.
(1)写出
在
上的表达式，并写出函数
在
上的单调区间(不用过程，直接写出即可)；
(2)求出
在
上的最小值与最大值，并求出相应的自变量的取值.
【答案】(1)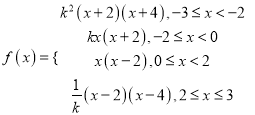 
， 
和
为增区间， 
为减区间.
(2) 
， 
.
【解析】试题分析：（1）根据函数关系，可求得
，根据函数的定义域可分
四段得到函数的解析式；根据分段函数的图像可求得函数的单调区间；（2）根据（1）函数的单调区间可知函数的最大值出自
，最小值出自
，再根据
的范围讨论最后的最大值和最小值.
试题解析：解：∵
，∴
，
∴
.
(1)当
时， 
，
，
当
时， 
，
，
当
时， 
，
，
综上： 
在
上的表达式为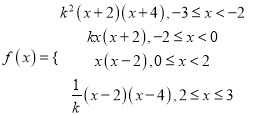
，
由于
，由
在
上的图象，可得
和
为增区间， 
为减区间.
(2)由(1)得
的最小值出自
， 
，
的最大值出自
， 
.
A.当
时， 
， 
，此时， 
最大值为
，最小值为
；
B.当
时， 
， 
，此时
最大值为1，最小值为
；
C.当
时， 
， 
；
此时： 
， 
.
练习册系列答案
相关题目
