Question

【题目】已知椭圆 ： 的离心率为 ，且过点 ， ， 是椭圆 上异于长轴端点的两点.
（1）求椭圆 的方程；
（2）已知直线 ： ，且 ，垂足为 ， ，垂足为 ，若 ，且 的面积是 面积的5倍，求 面积的最大值.

Answer 1

【答案】
（1）解：依题意 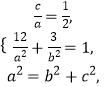解得

故椭圆 的方程为 .

（2）解：设直线 与 轴相交于点 ， ，

由于 且 ，

得 ， （舍去）或 ，

即直线 经过点 ，

设 ， ， 的直线方程为： ，

由 即 ，

， ，

，

令 ，所以 ，

因为 ，所以 在 上单调递增，所以在 上单调递增，

所以 ，所以 （当且仅当 ，即 时“ ”成立），

故 的最大值为3.

【解析】（1）由离心率和过已知点得到关于a,b,c的方程组求a,b,c得到椭圆方程。
（2）通过已知两个三角形面积的关系得到直线AB过定点，再设直线AB的方程，代入到椭圆方程中得到方程组，消去x得关于y的一元二次方程，由韦达定理及弦长公式将所求三角形面积表示为关于m的函数式，用均值不等式求最大值。