题目内容
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=4x-5 |
| C.y=-4x+3 | D. y=-3x+2 |
D
解析试题分析:由曲线y=x3-3x2+1,所以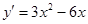 ,曲线
,曲线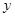
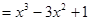 在点
在点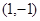 处的切线的斜率为:
处的切线的斜率为: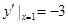 ,此处的切线方程为:
,此处的切线方程为: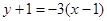 ,即
,即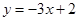 .
.
考点:利用导数研究曲线上某点切线方程.
点评:本题考查导数的几何意义、关键是求出直线的斜率,正确利用直线的点斜式方程,考查计算能力.

练习册系列答案
相关题目
曲线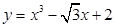 上的任意一点P处切线的斜率的取值范围是( )
上的任意一点P处切线的斜率的取值范围是( )
A.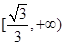 | B.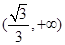 | C.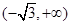 | D.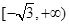 |
曲线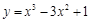 在点
在点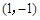 处的切线方程为
处的切线方程为
A.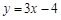 | B.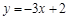 | C.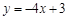 | D.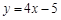 |
函数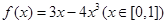 的最大值是( )
的最大值是( )
| A.1 | B.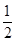 | C.0 | D.-1 |
曲线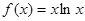 在点
在点 处的切线方程为 ( )
处的切线方程为 ( )
A. | B.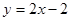 | C.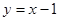 | D.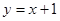 |
设连续函数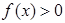 ,则当
,则当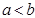 时,定积分
时,定积分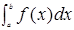 的符号
的符号
| A.一定是正的 |
| B.一定是负的 |
C.当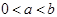 时是正的,当 时是正的,当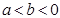 时是负的 时是负的 |
| D.以上结论都不对 |
设函数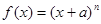 ,其中
,其中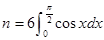 ,
, 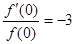 ,则
,则 的展开式中
的展开式中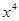 的系数为( )
的系数为( )
| A.-360 | B.360 | C.-60 | D.60 |
已知函数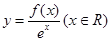 满足
满足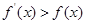 ,则
,则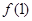 与
与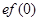 大小关系是( )
大小关系是( )
A.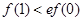 | B.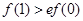 | C.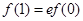 | D.不能确定 |
若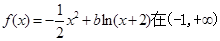 上是减函数,则
上是减函数,则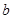 的取值范围是( )
的取值范围是( )
A. | B.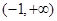 | C.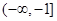 | D.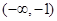 |