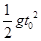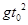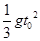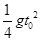题目内容
曲线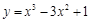 在点
在点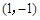 处的切线方程为
处的切线方程为
A.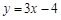 | B.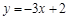 | C.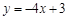 | D.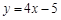 |
B
解析试题分析:先求出导函数,然后将x=1代入求出切线的斜率,利用点斜式求出直线的方程,最后化成一般式即可.解:因为曲线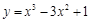 的导数为
的导数为 在点
在点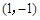 处的切线的斜率为-3,故切线方程为
处的切线的斜率为-3,故切线方程为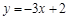 ,选B.
,选B.
考点:导数的几何意义
点评:本试题属于基础题,考查了导数几何意义的运用。

练习册系列答案
相关题目
积分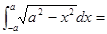 ( )
( )
A. | B.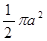 | C.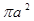 | D.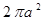 |
下列运算正确的是( )
A. x x | B.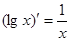 |
C. | D. |
.设三次函数 的导函数为
的导函数为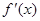 ,函数
,函数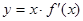 的图象的一部分如图所示,则正确的是
的图象的一部分如图所示,则正确的是 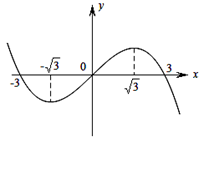
A. 的极大值为 的极大值为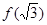 ,极小值为 ,极小值为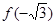 |
B. 的极大值为 的极大值为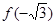 ,极小值为 ,极小值为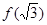 |
C. 的极大值为 的极大值为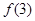 ,极小值为 ,极小值为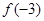 |
D. 的极大值为 的极大值为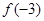 ,极小值为 ,极小值为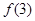 |
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=4x-5 |
| C.y=-4x+3 | D. y=-3x+2 |
函数 的导函数为( )
的导函数为( )
A. | B.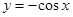 | C.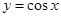 | D.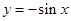 |
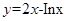 在点
在点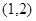 处的切线方程为( )
处的切线方程为( )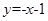 B.
B.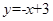 C.
C.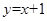 D.
D.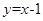
 是定义域为R的奇函数,且
是定义域为R的奇函数,且 ,
, 的图象如图所示。若正数
的图象如图所示。若正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )