题目内容
曲线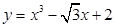 上的任意一点P处切线的斜率的取值范围是( )
上的任意一点P处切线的斜率的取值范围是( )
A.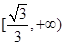 | B.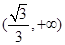 | C.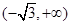 | D.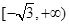 |
D
解析试题分析:先求导函数,进而可确定导函数的范围,利用导数的几何意义,可求曲线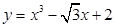 上的任意一点P处切线的斜率的取值范围解:由题意,f(x)=
上的任意一点P处切线的斜率的取值范围解:由题意,f(x)=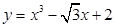 ,∴f/(x)=3x2-
,∴f/(x)=3x2- ≥-
≥- ∴曲线
∴曲线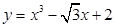 上的任意一点P处切线的斜率的取值范围是[-
上的任意一点P处切线的斜率的取值范围是[- ,+∞),故选D
,+∞),故选D
考点:导数的几何意义
点评:本题以函数为载体,考查导数的几何意义,解题的关键是求导函数,并确定函数的值域

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若 ,
, 满足
满足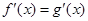 ,则
,则 与
与 满足
满足
A.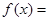  | B.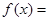 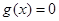 |
C.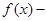  为常数函数 为常数函数 | D.  为常数函数 为常数函数 |
积分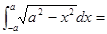 ( )
( )
A. | B.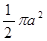 | C.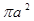 | D.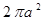 |
已知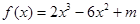 (
( 为常数)在
为常数)在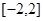 上有最大值
上有最大值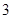 ,那么此函数在
,那么此函数在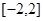 上的最小值为( )
上的最小值为( )
| A.-37 | B.-29 | C.-5 | D.-11 |
曲线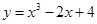 在点
在点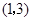 处的切线的倾斜角为( )
处的切线的倾斜角为( )
| A.30° | B.45° | C.60° | D.120° |
函数y=x2cosx的导数为( ).
| A.y′=2xcosx-x2sinx | B.y′=2xcosx+x2sinx |
| C. y′=x2cosx-2xsinx | D.y′=xcosx-x2sinx |
下列运算正确的是( )
A. x x | B.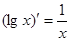 |
C. | D. |
.设三次函数 的导函数为
的导函数为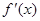 ,函数
,函数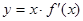 的图象的一部分如图所示,则正确的是
的图象的一部分如图所示,则正确的是 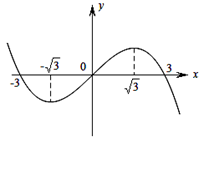
A. 的极大值为 的极大值为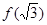 ,极小值为 ,极小值为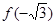 |
B. 的极大值为 的极大值为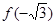 ,极小值为 ,极小值为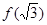 |
C. 的极大值为 的极大值为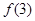 ,极小值为 ,极小值为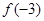 |
D. 的极大值为 的极大值为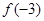 ,极小值为 ,极小值为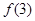 |
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=4x-5 |
| C.y=-4x+3 | D. y=-3x+2 |