题目内容
曲线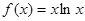 在点
在点 处的切线方程为 ( )
处的切线方程为 ( )
A. | B.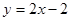 | C.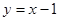 | D.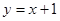 |
c
解析试题分析:∵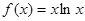 ,∴
,∴ ,故切线斜率
,故切线斜率 ,又点为(1,0),故切线方程为y-0=1(x-1)即y=x-1,故选C
,又点为(1,0),故切线方程为y-0=1(x-1)即y=x-1,故选C
考点:本题考查了切线方程的求法
点评: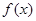 在
在 处导数
处导数 即为
即为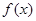 所表示曲线在
所表示曲线在 处切线的斜率,即
处切线的斜率,即 ,则切线方程为:
,则切线方程为: .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线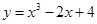 在点
在点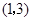 处的切线的倾斜角为( )
处的切线的倾斜角为( )
| A.30° | B.45° | C.60° | D.120° |
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=4x-5 |
| C.y=-4x+3 | D. y=-3x+2 |
曲线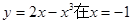 处的切线方程为( )
处的切线方程为( )
A.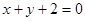 | B. |
C.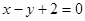 | D.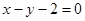 |
已知函数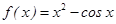 ,则
,则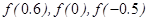 的大小关系是( )
的大小关系是( )
A.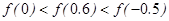 | B. |
C.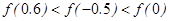 | D. |
若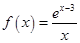 ,则
,则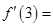 ( )
( )
A.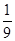 | B.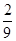 | C.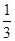 | D.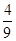 |
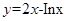 在点
在点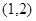 处的切线方程为( )
处的切线方程为( )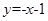 B.
B.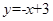 C.
C.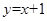 D.
D.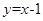
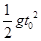
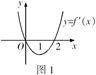
 是函数
是函数 的导函数,
的导函数, 的图象如图1所示,则
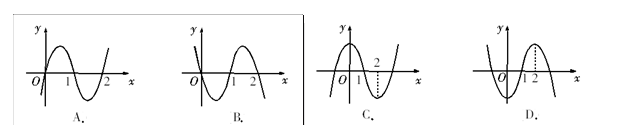
的图象如图1所示,则 的图象最有可能的是
的图象最有可能的是