题目内容
函数f(x)=sin(cosx)值域为 .
考点:正弦函数的定义域和值域
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:令t=cosx,x∈R,则-1≤t≤1,由正弦函数的增区间,计算即可得到所求值域.
解答:
解:令t=cosx,x∈R,
则-1≤t≤1,
由于[-1,1]⊆[-
,
],
且[-
,
]为y=sint的增区间,
则sin(-1)≤y≤sin1,
则值域为[-sin1,sin1].
故答案为:[-sin1,sin1].
则-1≤t≤1,
由于[-1,1]⊆[-
| π |
| 2 |
| π |
| 2 |
且[-
| π |
| 2 |
| π |
| 2 |
则sin(-1)≤y≤sin1,
则值域为[-sin1,sin1].
故答案为:[-sin1,sin1].
点评:本题考查余弦函数的值域,考查正弦函数的单调区间及单调性的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
直线l:2x+3y+6=0的斜率和在y轴上的截距分别为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
某县有甲,乙,丙,丁,戊五所中国农业银行分行,总行设在甲银行为保证资金安全,国家规定,每天下午五点都从总行出发一次收款至其它分行然后回到总部,第二天早上9点再从总行出发依次送款至各个分行,八一建军节早晨,该小李值班送款,问小李的不同的送款方式共有( )
| A、20 | B、12 | C、24 | D、16 |
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
A、(-3,-
| ||||
B、(-
| ||||
C、(-3,-
| ||||
| D、(-3,-1) |
若向量
=(1,2),
=(3,4),则
-
=( )
| a |
| b |
| b |
| a |
| A、(4,6) |
| B、(-4,-6) |
| C、(2,2) |
| D、(-2,-2) |
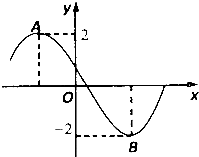 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,