题目内容

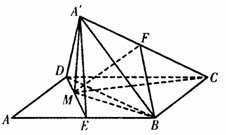
如图，在平行四边形ABCD中，AB＝2BC＝4，∠ABC＝120°，E为AB的中点，将△ADE沿直线DE翻折成△DE，F为C的中点，C＝4．     

   （Ⅰ）求证：平面DE⊥平面BCD；

（Ⅱ）求证：BF∥平面DE．

证明：（Ⅰ）证由题意得是沿翻转而成，所以≌，

，四边形是平形四边形，

，

又

和都是等边三角形.

是的中点,

由在中,

在中, …………………3分

是直角三角形,

又

平面

又平面

平面平面…………………………………………………………6分

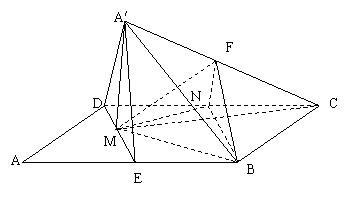
(Ⅱ)选取的中点,连接

点分别是中点,∥………………8分

又点分别是平行四边形的的中点,

∥………………………………………………………………………10分

又

平面∥平面

平面

∥平面……………………………………………………………12分

练习册系列答案
相关题目
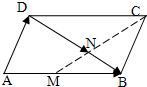
精英家教网如图，在平行四边形ABCD中，下列结论中错误的是（　　）
A、
AB
=
DC
B、
AD
+
AB
=
AC
C、
AB
-
AD
=
BD
D、
AD
+
CB
=
0
精英家教网如图，在平行四边形ABCD，
AD
=a，
AB
=b，M为AB的中点，点N在DB上，且
DN
=t
NB
．
（1）当t=2时，证明：M、N、C三点共线；
（2）若M、N、C三点共线，求实数t的值．
如图，在平行四边形ABCD中，
AB
=
a
，
AD
=
b
，
AN
=3
NC
，则
BN
=
-
1
4
a
+
3
4
b
-
1
4
a
+
3
4
b
（用
a
，
b
表示）
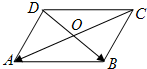如图，在平行四边形ABCD中，若
OA
=
a
，
OB
=
b
则下列各表述是正确的为（　　）
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的中点．
（1）求AB所在直线的一般式方程；
（2）求直线CD与直线AB所成夹角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网