题目内容
13．
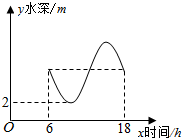如图，某港口一天6时到18时的水深变化曲线近似满足函数y=sin（$\frac{π}{6}$x+φ）+k，据此函数可知，这段时间水深（单位：m）的最大值为4．
分析 由题意和最小值易得k的值，进而可得最大值．
解答 解：由题意可得当sin（$\frac{π}{6}$x+φ）取最小值-1时，
函数取最小值ymin=-1+k=2，解得k=3，
∴y=sin（$\frac{π}{6}$x+φ）+3，
∴当sin（$\frac{π}{6}$x+φ）取最大值1时，
函数取最大值ymax=1+3=4，
故答案为：4．
点评 本题考查三角函数的图象和性质，涉及三角函数的最值，属基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
8．若（4k+1）•180°＜α＜（4k+1）•180°+60°（k∈Z），则α所在象限为（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
5．在直角坐标系中，直线3x-$\sqrt{3}$y+1=0的倾斜角是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |