题目内容
已知a,b,c分别为△ABC的三个内角∠A,∠B,∠C的对边,且
c=asinC+
ccosA;
(1)求∠A的大小;
(2)若a=2
,△ABC的面积为2
,求b,c的值.
| 3 |
| 3 |
(1)求∠A的大小;
(2)若a=2
| 2 |
| 3 |
考点:余弦定理,正弦定理
专题:计算题,三角函数的求值,解三角形
分析:(1)运用正弦定理和二倍角的正弦和余弦公式,以及同角的商数关系,结合特殊角的三角函数值,即可得到A;
(2)由余弦定理和面积公式,联立方程,即可解得b,c.
(2)由余弦定理和面积公式,联立方程,即可解得b,c.
解答:
解:(1)由正弦定理,可得,
c=asinC+
ccosA,
即为
sinC=sinAsinC+
sinCcosA,
即sinA=
(1-cosA),即2sin
cos
=2
sin2
,
即有tan
=
,由于0<A<π,即有
=
,
则A=
;
(2)由△ABC的面积为2
,则2
=
bcsin
=
bc,
即有bc=8,
由余弦定理,可得,
a2=8=b2+c2-2bccos
=b2+c2-bc=b2+c2-8
即b2+c2=16,
解得,b=c=2
.
| 3 |
| 3 |
即为
| 3 |
| 3 |
即sinA=
| 3 |
| A |
| 2 |
| A |
| 2 |
| 3 |
| A |
| 2 |
即有tan
| A |
| 2 |
| ||
| 3 |
| A |
| 2 |
| π |
| 6 |
则A=
| π |
| 3 |
(2)由△ABC的面积为2
| 3 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
即有bc=8,
由余弦定理,可得,
a2=8=b2+c2-2bccos
| π |
| 3 |
即b2+c2=16,
解得,b=c=2
| 2 |
点评:本题考查正弦定理和余弦定理、及面积公式的运用,考查三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知{an}{bn}满足
an=A
bn=B,其中A,B为确定的常数,给出两个命题:甲:对于任意n∈N*,an<bn则A<B;乙:若A<B则存在n0∈N*当n>n0时,an<bn恒成立.( )
| lim |
| n→∞ |
| lim |
| n→∞ |
| A、甲是假命题,乙是假命题 |
| B、甲是假命题,乙是真命题 |
| C、甲是真命题,乙是假命题 |
| D、甲是真命题,乙是真命题 |
函数f(x)=log2(-x2+x+6)的单调减区间是( )
A、(-∞,
| ||
B、[
| ||
C、(-2,
| ||
D、(
|
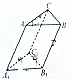 已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.
已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.