题目内容
(14分)已知函数 .
.
(1)若 ,求
,求 的值域;
的值域;
(2)若存在实数t,当 ,
, 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)函数的对称轴为 ,研究函数的值域可分三种情况讨论对称轴的位置:对称轴在
,研究函数的值域可分三种情况讨论对称轴的位置:对称轴在 的左侧,内部,右侧;(2)将
的左侧,内部,右侧;(2)将 在
在 恒成立,转化为
恒成立,转化为 恒成立,即
恒成立,即 在
在 上的最大值
上的最大值 恒成立,由
恒成立,由 恒成立知
恒成立知 ,
,
化简得 ,
,
令 ,则原题可转化为:存在
,则原题可转化为:存在 ,使得
,使得 。
。
即当 时,
时, ,再讨论
,再讨论 的对称轴为
的对称轴为 ,在
,在 的左侧,在
的左侧,在 内
内
讨论m的取值范围.
试题解析:(1)由题意得
当 时,
时, ,
, ,
,
∴此时 的值域为
的值域为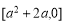 。
。
当 时,
时, ,
, ,
,
∴此时 的值域为
的值域为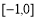 。
。
当 时,
时, ,
, ,
,
∴此时 的值域为
的值域为 。
。
(2)由 恒成立得
恒成立得 恒成立。
恒成立。
令 ,
, ,因为抛物线的开口向上,
,因为抛物线的开口向上,
所以 。
。
由 恒成立知
恒成立知 ,化简得
,化简得
令 ,则原题可转化为:存在
,则原题可转化为:存在 ,使得
,使得 。
。
即当 时,
时, 。
。
∵ ,
, 的对称轴为
的对称轴为 。
。
①当 ,即
,即 时,
时,
∴ ,解得
,解得
②当 ,即
,即 时,
时,
∴ ,解得
,解得
综上, 的取值范围为
的取值范围为 .
.
考点:1、函数的值域;2、不等式恒成立.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (y≠0) (B)
(y≠0) (B) (y≠0)
(y≠0) (y≠0) (D)
(y≠0) (D) (y≠0)
(y≠0) (
( )为奇函数,
)为奇函数, ,
, ,则
,则
 D.5
D.5 的解集为
的解集为 ,则
,则 .
. 的值域是( )
的值域是( )  B.
B. C.
C.  D.
D. 
 .
. ;
; ,
, ,求△ABC的面积.
,求△ABC的面积. ,
, 分别是R上的奇函数,偶函数,且满足
分别是R上的奇函数,偶函数,且满足 ,则有
,则有 B.
B.
 D.
D.

 则
则 ”的逆否命题是____________
”的逆否命题是____________