题目内容
6.求曲线y2=4x与直线y=x所围成的图形绕x轴旋转一周所得旋转体的体积( )| A. | $\frac{8}{3}$ | B. | $\frac{32}{3}$π | C. | $\frac{8}{3}$π | D. | 24π |
分析 利用定积分求体积.
解答 解:解方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=x}\end{array}\right.$得x=4,y=4.
∴几何体的体积V=π${∫}_{0}^{4}$(4x-x2)dx=π•(2x2-$\frac{{x}^{3}}{3}$)|${\;}_{0}^{4}$=$\frac{32π}{3}$.
故选B.
点评 本题考查用定积分求简单几何体的体积,属于基础题.利用定积分求旋转体的体积,求解的关键是找出被积函数和相应的积分区间,准确利用公式进行计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.第一组样本点为(-5,-8.9),(-4,-7.2),(-3,-4.8),(-2,-3.3),(-1,-0.9)
第二组样本点为(1,8.9),(2,7.2),(3,4.8),(4,3.3),(5,0.9)
第一组变量的线性相关系数为r1,第一组变量的线性相关系数为r2,则( )
第二组样本点为(1,8.9),(2,7.2),(3,4.8),(4,3.3),(5,0.9)
第一组变量的线性相关系数为r1,第一组变量的线性相关系数为r2,则( )
| A. | r1>0>r2 | B. | r2>0>r1 | C. | r1<r2<0 | D. | r2>r1>0 |
11.若实数a,b,c∈(0,1)且10a+9b=9,a+b+c=1,则当$\frac{10}{a}+\frac{1}{9b}$取最小值时,c的值为( )
| A. | $\frac{5}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{1}{11}$ | D. | 0 |
15.设集合M={x2-2x<0},N={x|x≤1},则M∩N=( )
| A. | (0,1) | B. | (1,2) | C. | (0,2) | D. | (0,1] |
16.设${\vec e}_1,{\vec e}_2$是两个单位向量,则下列结论正确的是( )
| A. | ${\vec e}_1={\vec e}_2$ | B. | ${\vec e}_1∥{\vec e}_2$ | C. | $|{{\vec e}_1}|=|{{\vec e}_2}|$ | D. | 以上都不对 |
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,M为PD的中点.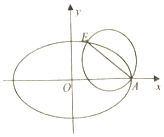 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.