题目内容
20.已知函数f(x)=9-2|x|,g(x)=x2+1,构造函数F(x)=$\left\{\begin{array}{l}{g(x),f(x)>g(x)}\\{f(x),g(x)≥f(x)}\end{array}\right.$,那么函数y=F(x)的最大值为5.分析 由g(x)-f(x)=x2-8+2|x|≥0得|x|≥2,从而可得F(x)=$\left\{\begin{array}{l}{{x}^{2}+1,|x|≤2}\\{9-2|x|,|x|>2}\end{array}\right.$,即可求出函数y=F(x)的最大值.
解答 解:由g(x)-f(x)=x2-8+2|x|≥0得|x|≥2;
故F(x)=$\left\{\begin{array}{l}{{x}^{2}+1,|x|≤2}\\{9-2|x|,|x|>2}\end{array}\right.$,
故|x|=2时,有最大值5.
故答案为:5.
点评 本题考查了分段函数,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
11.正四面体ABCD的外接球半径为6,过棱AB作该球的截面,则截面面积的最小值为( )
| A. | 9π | B. | 4π | C. | 24π | D. | 16π |
5.复数$\frac{i}{1-2i}$=( )
| A. | $\frac{-2+i}{5}$ | B. | $\frac{-2-i}{5}$ | C. | $\frac{2-i}{5}$ | D. | $\frac{2+i}{5}$ |
12.幂函数y=f(x)的图象经过点A(2,4),则曲线y=f(x)在点A处切线的斜率为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
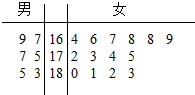 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.