题目内容

11．正四面体ABCD的外接球半径为6，过棱AB作该球的截面，则截面面积的最小值为（　　）
A．9πB．4πC．24πD．16π

分析 将四面体ABCD放置于正方体中，则正方体的外接球就是四面体ABCD的外接球．因此利用题中数据算出AB，即可算出截面面积的最小值．

解答 解：由题意，面积最小的截面是以AB为直径的截面，
将四面体ABCD放置于正方体中，可得正方体的外接球就是四面体ABCD的外接球，
设AB=a，则$\sqrt{3}•\frac{\sqrt{2}}{2}a$=12，可求得a=4$\sqrt{6}$，
进而截面面积的最小值为$π•（2\sqrt{6}）^{2}$=24π．
故选：C．

点评 球的内接几何体问题是高考热点问题，本题通过求球的截面面积，对考生的空间想象能力及运算求解能力进行考查，具有一定难度．

练习册系列答案
相关题目
1．若过点A（2，m）可作函数f（x）=x3-3x对应曲线的三条切线，则实数m的取值范围（　　）
A．[-2，6]B．（-6，1）C．（-6，2）D．（-4，2）
2．$已知z为复数，\frac{z}{1-i}=3+i，则|z|$=（　　）
A．$2\sqrt{5}$B．$5\sqrt{2}$C．5D．2
19．棱长为1的正方体ABCD-A1B1C1D1中，点P在平面ABCD上，满足PC1=3PA，则点P的轨迹为（　　）
A．直线B．一段圆弧C．椭圆D．圆
6．已知圆C过点P（$\sqrt{2}$，0）且与圆M：（x+4）2+（y+4）2=r2（r＞0），关于直线x+y+4=0对称．
（1）求圆C的方程；
（2）过点R（1，1）作两条相异直线分别与圆C相交于A、B，且直线RA和直线RB的倾斜角互补，O为坐标原点，试判断直线OR和直线AB是否平行，并说明理由．
16．已知圆C过点P（$\sqrt{2}$，0）且与圆M：（x+4）2+（y+4）2=r2（r＞0）关于直线x+y+4=0对称，定点R的坐标为（1，-1）
（1）求圆C的方程；
（2）设Q为圆上的一个动点，求$\overrightarrow{PQ}$•$\overrightarrow{MQ}$的最小值；
（3）过点P作两条相异直线分别与圆C相交于A、B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和直线AB是否平行，并说明理由．
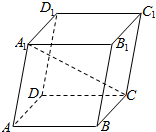3．如图所示的平行六面体ABCD-A1B1C1D中，AB=AD=AA1=1，∠BAD=90°，∠BAA1=∠DAA1=60°，则CA1的长=1．
20．已知函数f（x）=9-2|x|，g（x）=x2+1，构造函数F（x）=$\left\{\begin{array}{l}{g（x），f（x）＞g（x）}\\{f（x），g（x）≥f（x）}\end{array}\right.$，那么函数y=F（x）的最大值为5．
1．定义在区间[x1，x2]长度为x2-x1（x2＞x1），已知函数f（x）=$\frac{（{a}^{2}+a）x-2}{{a}^{2}x}$（a∈R，a≠0）的定义域与值域都是[m，n]，则区间[m，n]取最长长度时a的值是7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网