题目内容
设数列 满足:
满足: ,
, ,
, .
.
(Ⅰ)求 的通项公式及前
的通项公式及前 项和
项和 ;
;
(Ⅱ)已知 是等差数列,
是等差数列, 为前
为前 项和,且
项和,且 ,
, .求
.求 的通项公式,并证明:
的通项公式,并证明: .
.
 满足:
满足: ,
, ,
, .
.(Ⅰ)求
 的通项公式及前
的通项公式及前 项和
项和 ;
;(Ⅱ)已知
 是等差数列,
是等差数列, 为前
为前 项和,且
项和,且 ,
, .求
.求 的通项公式,并证明:
的通项公式,并证明: .
.(Ⅰ) ,
, ;(Ⅱ)
;(Ⅱ) ,证明详见解析.
,证明详见解析.
 ,
, ;(Ⅱ)
;(Ⅱ) ,证明详见解析.
,证明详见解析.试题分析:(Ⅰ)求
 的通项公式及前
的通项公式及前 项和
项和 ,由已知
,由已知 ,
, ,
, ,数列
,数列 是以
是以 为首项,
为首项, 为公比等比数列,由等比数列的通项公式及前
为公比等比数列,由等比数列的通项公式及前 项和公式可得;(Ⅱ)求
项和公式可得;(Ⅱ)求 的通项公式,由
的通项公式,由 是等差数列,
是等差数列, 为前
为前 项和,且
项和,且 ,
, ,可设等差数列
,可设等差数列 的公差为
的公差为 ,根据已知条件,求出公差
,根据已知条件,求出公差 的值,从而得到
的值,从而得到 ;证明:
;证明: ,由
,由 ,分母是等差数列连续两项积,像这类数列,求其前
,分母是等差数列连续两项积,像这类数列,求其前 项和,常常采用拆项相消法,即
项和,常常采用拆项相消法,即 ,从而解出.
,从而解出.试题解析:(Ⅰ)因为
 ,又
,又 ,所以
,所以 ,因此
,因此 是首项为1,公比为3的等比数列,所以
是首项为1,公比为3的等比数列,所以 ,
, ;
;(Ⅱ)设等差数列
 的公差为
的公差为 ,依题意
,依题意 ,
, ,所以
,所以 ,即
,即 ,故
,故 . 由此得,
. 由此得, . 所以,
. 所以,

 .因此所证不等式成立.
.因此所证不等式成立.  项和,考查学生的运算能力以及转化与化归的能力.
项和,考查学生的运算能力以及转化与化归的能力.
练习册系列答案
相关题目
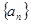 中,
中,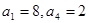 且满足
且满足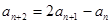 (
( 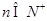 )
)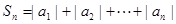 ,求
,求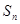 ;
;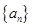 的前三项依次为
的前三项依次为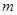 、4、
、4、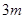 ,前
,前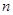 项和为
项和为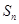 ,且
,且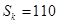 .
.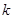 的值;
的值;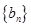 的通项
的通项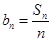 ,证明数列
,证明数列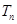 .
.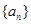 公比为
公比为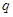 ,其前
,其前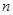 项和为
项和为 ,若
,若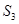 、
、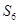 、
、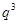 等于( )
等于( )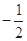
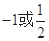
 满足:
满足: ,且对任意的正整数
,且对任意的正整数 ,
, 都有
都有 ,则数列
,则数列 = .
= .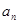 }中,各项都是正数,且a1,
}中,各项都是正数,且a1, 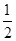 a3,2a2成等差数列,则
a3,2a2成等差数列,则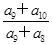 =( )
=( )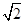
 是等差数列,
是等差数列, ,其中
,其中 ,则此数列的前
,则此数列的前 项和
项和 _______ .
_______ .