题目内容
已知等差数列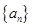 的前三项依次为
的前三项依次为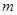 、4、
、4、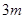 ,前
,前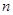 项和为
项和为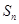 ,且
,且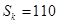 .
.
(1)求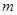 及
及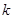 的值;
的值;
(2)设数列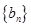 的通项
的通项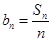 ,证明数列
,证明数列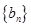 是等差数列,并求其前
是等差数列,并求其前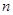 项和
项和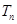 .
.
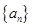 的前三项依次为
的前三项依次为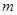 、4、
、4、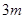 ,前
,前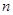 项和为
项和为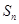 ,且
,且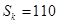 .
.(1)求
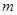 及
及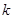 的值;
的值;(2)设数列
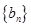 的通项
的通项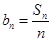 ,证明数列
,证明数列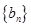 是等差数列,并求其前
是等差数列,并求其前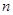 项和
项和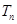 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)等差数列
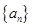 的前三项依次为
的前三项依次为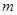 、4、
、4、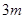 ,由等差中项性质可求出
,由等差中项性质可求出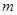 ,从而得到前
,从而得到前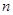 项和为
项和为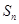 ,再由
,再由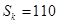 即可求出
即可求出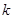 的值;(2)由
的值;(2)由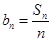 ,可得
,可得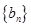 的通项公式,从而得出
的通项公式,从而得出 ,即证明了数列
,即证明了数列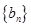 是等差数列,再由等差数列前
是等差数列,再由等差数列前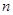 项和可以求出
项和可以求出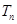 .
.试题解析:(1)等差数列
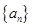 的前三项依次为
的前三项依次为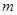 、4、
、4、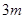 ,所以4是
,所以4是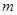 、
、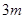 的等差中项,
的等差中项, ,
,
 .所以等差数列的前三项依次为2、4、6,所以首项
.所以等差数列的前三项依次为2、4、6,所以首项 为2,公差为2.所以等差数列
为2,公差为2.所以等差数列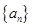 前
前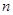 项和
项和 .由
.由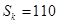 得
得 ,又
,又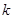 为正整数,
为正整数, . 7分
. 7分(2)由上问得
 ,
, ,
, ,所以
,所以 ,数列
,数列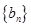 是等差数列 9分
是等差数列 9分  ,
, ,由等差数列前
,由等差数列前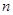 项和公式,
项和公式, . 14分
. 14分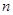 项和;3.等差数列的定义.
项和;3.等差数列的定义.
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
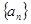 的前
的前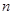 项和为
项和为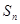 ,已知
,已知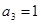 ,
,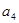 是
是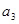 和
和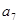 的等比中项.
的等比中项.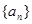 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中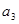 是
是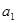 与
与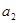 的等差中项.
的等差中项. 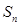
 中,
中, (
( ).
). 的值;
的值; ,使得数列
,使得数列 是一个等差数列?若存在,求
是一个等差数列?若存在,求 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由. 满足:
满足: ,
, ,
, .
. 项和
项和 ;
; 是等差数列,
是等差数列, 为前
为前 ,
, .求
.求 的通项公式,并证明:
的通项公式,并证明: .
.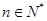 (
(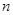 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前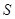 型数列。
型数列。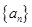 是首项
是首项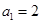 的
的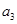 的值;
的值;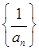 是
是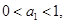 试求
试求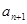 与
与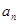 的递推关系,并证明
的递推关系,并证明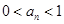 对
对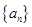 中,
中,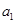 、
、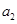 、
、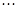 、
、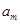 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,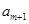 、
、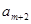 、
、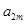 ,构成首项为
,构成首项为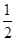 ,公比为
,公比为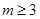 ,
,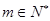 .
.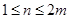 ,
,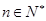 ,都有
,都有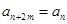 成立.
成立.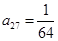 时,求
时,求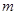 的值;
的值;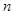 项和为
项和为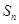 .判断是否存在
.判断是否存在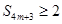 成立?若存在,求出
成立?若存在,求出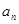 }的前n项和为
}的前n项和为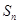 ,且
,且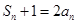 ,则使不等式
,则使不等式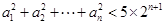 成立的n的最大值为 .
成立的n的最大值为 .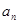 }是等差数列,a4+a6=6,其前5项和S5=10,则其公差d=___________.
}是等差数列,a4+a6=6,其前5项和S5=10,则其公差d=___________.