题目内容
数列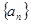 中,
中,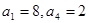 且满足
且满足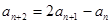 (
( 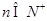 )
)
(Ⅰ)求数列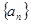 的通项公式;
的通项公式;
(Ⅱ)设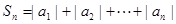 ,求
,求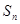 ;
;
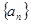 中,
中,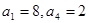 且满足
且满足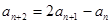 (
( 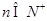 )
)(Ⅰ)求数列
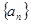 的通项公式;
的通项公式;(Ⅱ)设
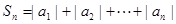 ,求
,求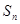 ;
;(Ⅰ) ;(Ⅱ)
;(Ⅱ)

 ;(Ⅱ)
;(Ⅱ)

试题分析:(Ⅰ)首先把地推关系
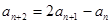 变形为
变形为 ,从而证明数列
,从而证明数列 为等差数列,再求出公差
为等差数列,再求出公差 ,利用等差数列的通项公式可求得结果.
,利用等差数列的通项公式可求得结果.(Ⅱ)因为本题需要去掉绝对值符号,所以要知道
 的符号,从而找到引起分类讨论的原因,分
的符号,从而找到引起分类讨论的原因,分 和
和 两种情况,分别去掉绝对值符号,利用等差数列的前
两种情况,分别去掉绝对值符号,利用等差数列的前 和公式求出结果.
和公式求出结果.试题解析:(Ⅰ)由题意,
 ,
, 为等差数列,设公差为
为等差数列,设公差为 ,
,由题意得
 ,
, .
.(Ⅱ)若
 ,
,

 时,
时,

故


 项和.
项和.
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
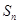 为数列
为数列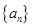 的前
的前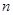 项和,对任意的
项和,对任意的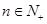 ,都有
,都有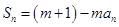 (
(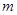 为正常数).
为正常数).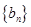 满足
满足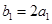 ,
,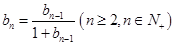 ,求数列
,求数列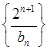 的前
的前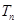 .
.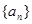 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中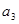 是
是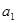 与
与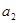 的等差中项.
的等差中项. 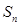
 中,
中, (
( ).
). 的值;
的值; ,使得数列
,使得数列 是一个等差数列?若存在,求
是一个等差数列?若存在,求 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由. 满足:
满足: ,
, ,
, .
. 项和
项和 ;
; 是等差数列,
是等差数列, 为前
为前 ,
, .求
.求 的通项公式,并证明:
的通项公式,并证明: .
.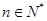 (
(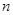 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前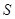 型数列。
型数列。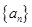 是首项
是首项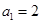 的
的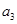 的值;
的值;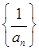 是
是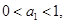 试求
试求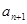 与
与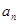 的递推关系,并证明
的递推关系,并证明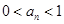 对
对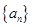
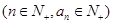 ,若
,若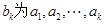 中最大值
中最大值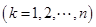 ,则称数列
,则称数列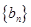 为数列
为数列 的通项公式
的通项公式 ,记
,记 ,试计算
,试计算 ,推测
,推测 .
. 的首项
的首项 公比
公比 ,则
,则 ( )
( )