题目内容
已知等比数列{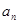 }中,各项都是正数,且a1,
}中,各项都是正数,且a1, 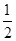 a3,2a2成等差数列,则
a3,2a2成等差数列,则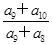 =( )
=( )
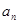 }中,各项都是正数,且a1,
}中,各项都是正数,且a1, 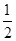 a3,2a2成等差数列,则
a3,2a2成等差数列,则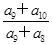 =( )
=( )A.1-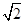 | B.1+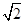 | C.2 | D.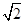 -1 -1 |
B
试题分析:由
 成等差数列得:
成等差数列得:  ,即
,即 ,从而
,从而 ,解得,
,解得, ,又因为各项都是正数,故
,又因为各项都是正数,故 ,而
,而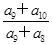
 ,故选B.
,故选B.
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
题目内容
 }中,各项都是正数,且a1,
}中,各项都是正数,且a1, 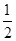 a3,2a2成等差数列,则
a3,2a2成等差数列,则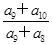 =( )
=( )A.1-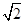 | B.1+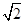 | C.2 | D.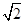 -1 -1 |
 成等差数列得:
成等差数列得:  ,即
,即 ,从而
,从而 ,解得,
,解得, ,又因为各项都是正数,故
,又因为各项都是正数,故 ,而
,而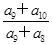
 ,故选B.
,故选B.
 53天天练系列答案
53天天练系列答案