题目内容
3.已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(-2,0),点$B({2,\;\;\sqrt{2}})$在椭圆C上.(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N.
求证:以MN为直径的圆必过椭圆的两焦点.
分析 (1)由题意可设椭圆标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$,结合已知及隐含条件列关于a,b,c的方程组,求解方程组得到a2,b2的值,则椭圆方程可求;
(2)设F(x0,y0),E(-x0,-y0),写出AE、AF所在直线方程,求出M、N的坐标,得到以MN为直径的圆的方程,由圆的方程可知以MN为直径的圆经过定点(±2,0).
解答 (1)解:(1)由题意可设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$,
则$\left\{\begin{array}{l}{c=2}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1}\end{array}\right.$,解得:a2=8,b2=4.
∴椭圆C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)证明:如图,设F(x0,y0),E(-x0,-y0),
则$\frac{{{x}_{0}}^{2}}{8}$+$\frac{{{y}_{0}}^{2}}{4}$=1,即有y02=$\frac{1}{2}$(8-x02),
A(-2$\sqrt{2}$,0),
AF所在直线方程y=$\frac{{y}_{0}}{{x}_{0}+2\sqrt{2}}$(x+2$\sqrt{2}$),
取x=0,得y=$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}+2\sqrt{2}}$,
∴N(0,$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}+2\sqrt{2}}$),
AE所在直线方程为y=$\frac{{y}_{0}}{{x}_{0}-2\sqrt{2}}$(x+2$\sqrt{2}$),
取x=0,得y=$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}-2\sqrt{2}}$,
∴M(0,$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}-2\sqrt{2}}$),
则以MN为直径的圆的圆心坐标为(0,$\frac{-2\sqrt{2}{x}_{0}{y}_{0}}{8-{{x}_{0}}^{2}}$),
半径r=$\frac{8{y}_{0}}{8-{{x}_{0}}^{2}}$,
圆的方程为x2+(y-$\frac{-2\sqrt{2}{x}_{0}{y}_{0}}{8-{{x}_{0}}^{2}}$)2=$\frac{64{{y}_{0}}^{2}}{(8-{{x}_{0}}^{2})^{2}}$=$\frac{16}{{{y}_{0}}^{2}}$,
即x2+(y+$\frac{\sqrt{2}{x}_{0}}{{y}_{0}}$)2=$\frac{16}{{{y}_{0}}^{2}}$,
取y=0,得x=±2.
∴以MN为直径的圆经过定点(±2,0),即为椭圆的焦点.
点评 本题考查椭圆的方程和简单性质,考查圆的方程的求法及应用,考查化简整理的运算能力,是中档题.

| 优秀 | 一般 | 合计 | |
| 男生 | 7 | 6 | |
| 女生 | 5 | 12 | |
| 合计 |
(2)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机抽取3人,用ξ表示所选3人中优秀的人数,试写出ξ的分布列,并求出ξ的数学期望,.${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d
独立性检验临界表:
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | (-3,4) | B. | (-3,-4) | C. | (3,4) | D. | (3,-4) |
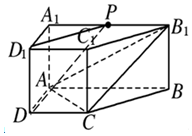 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点