题目内容
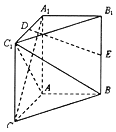
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
【答案】![]()
![]()
【解析】
(1).要求球![]() 的表面积的最小值,需求出球
的表面积的最小值,需求出球![]() 的表面积的算式,为此又需求出球
的表面积的算式,为此又需求出球![]() 的半径,从而根据算式的特点,用函数的单调性或不等式求出最小值.
的半径,从而根据算式的特点,用函数的单调性或不等式求出最小值.
(2).列出四棱锥![]() 的体积的算式,求出体积取得最大值时变量的取值,从而求出二面角
的体积的算式,求出体积取得最大值时变量的取值,从而求出二面角![]() 的正切值.
的正切值.
(1).设![]() ,则
,则![]() .∵
.∵![]() 平面
平面![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,
,
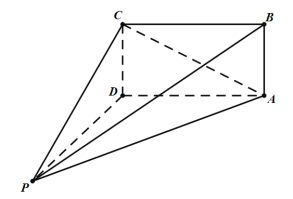
则四棱锥![]() 可补形成一个长方体,球
可补形成一个长方体,球![]() 的球心为
的球心为![]() 的中点,
的中点,
从而球![]() 的表面积为
的表面积为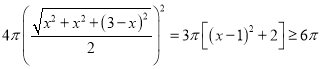 .
.
(2).四棱锥![]() 的体积
的体积![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() ,此时
,此时![]() ,
,![]() .
.
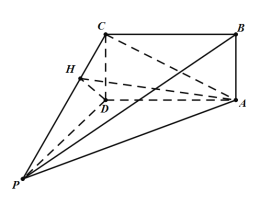
过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∵![]() ,∴
,∴![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目