题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性.
的单调性.
(2)试问是否存在![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)见解析;(2) 存在;![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)![]() ,
,![]() ,
,
所以![]() 得
得![]() ,所以通过对
,所以通过对![]() 与
与![]() 的大小关系进行分类讨论得
的大小关系进行分类讨论得![]() 的单调性;
的单调性;
(2)假设存在满足题意的![]() 的值,由题意需
的值,由题意需![]() ,所以由(1)的单调性求
,所以由(1)的单调性求![]() 即可;
即可;
又因为![]() 对
对![]() 恒成立,所以可以考虑从区间
恒成立,所以可以考虑从区间![]() 内任取一个
内任取一个![]() 值代入,解出
值代入,解出![]() 的取值范围,从而将
的取值范围,从而将![]() 的范围缩小减少讨论.
的范围缩小减少讨论.
解:(1)![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.
上单调递增.
(2)假设存在![]() ,使得
,使得![]() 对
对![]() 恒成立.
恒成立.
则![]() ,即
,即![]() ,
,
设![]() ,则存在
,则存在![]() ,使得
,使得![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以
,所以![]() 时
时![]() 即
即![]() .
.
又因为![]() 对
对![]() 恒成立时,需
恒成立时,需![]() ,
,
所以由(1)得:
当![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
且![]() 成立,从而
成立,从而![]() 满足题意.
满足题意.
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增,
上单调递增,
所以
所以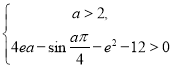 (*)
(*)
设![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,
所以![]() 的零点小于2,从而不等式组(*)的解集为
的零点小于2,从而不等式组(*)的解集为![]() ,
,
所以![]() 即
即![]() .
.
综上,存在![]() ,使得
,使得![]() 对
对![]() 恒成立,且
恒成立,且![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据以上数据完成下列![]() 列联表:
列联表:
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关?并写出简要分析.
参考公式和数据: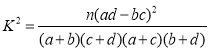 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |