题目内容
13.以双曲线$\frac{x^2}{4}-\frac{y^2}{12}=-1$的焦点为顶点,顶点为焦点的椭圆方程是( )| A. | $\frac{x^2}{4}+\frac{y^2}{m}=1$ | B. | $\frac{x^2}{m}-\frac{y^2}{2}=1$ | C. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}+\frac{y^2}{16}=1$ |
分析 求得双曲线的标准方程,则求得焦点和顶点坐标,即可求得a和c,则b2=a2-c2,即可求得椭圆的标准方程.
解答 解:双曲线$\frac{x^2}{4}-\frac{y^2}{12}=-1$的标准方程:$\frac{{y}^{2}}{12}-\frac{{x}^{2}}{4}=1$,则双曲线的焦点在x轴上,焦点坐标为(0,-4),(0,4),顶点坐标为(0,-2$\sqrt{3}$),(0,2$\sqrt{3}$),
由题意设椭圆的标准方程:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),
则a=4,c=2$\sqrt{3}$,b2=a2-c2=4,
∴椭圆的标准方程:$\frac{{y}^{2}}{16}+\frac{{x}^{2}}{4}=1$,
故选:D.
点评 本题考查椭圆的标准方程,考查双曲线的简单几何性质,属于基础题.

练习册系列答案
相关题目
10.已知z满足$({1-i})z=\sqrt{3}+i$(i为虚数单位),则|z|=( )
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 2 | D. | 1 |
5.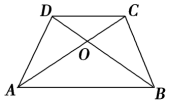 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.已知△ABC的顶点A(0,-4)、B(0,4),且4(sinB-sinA)=3sinC,则顶点C的轨迹方程是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1(x>3) | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1(x<-7) | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y>3) | D. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y<-3) |