题目内容
16.函数y=2-3x-$\frac{4}{x}$(x>0)的最值情况是( )| A. | 有最小值2-4$\sqrt{3}$ | B. | 有最大值2-4$\sqrt{3}$ | C. | 有最小值2+4$\sqrt{3}$ | D. | 有最大值2+4$\sqrt{3}$ |
分析 利用基本不等式的性质即可得出.
解答 解:∵x>0,∴$3x+\frac{4}{x}$≥2$\sqrt{3x•\frac{4}{x}}$=4$\sqrt{3}$.当且仅当x=$\frac{2\sqrt{3}}{3}$时取等号.
∴y≤2-4$\sqrt{3}$,即函数y=2-3x-$\frac{4}{x}$(x>0)有最大值2-4$\sqrt{3}$,而无最小值.
故选:B.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.在△ABC中,$a=2\sqrt{2},b=3,A=45°$,则此三角形解的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
11.函数f(x)=x3-x2-x(0<x<2)极小值是( )
| A. | 0 | B. | -1 | C. | 2 | D. | 1 |
1.若|$\frac{x}{x+1}$|>$\frac{x}{x+1}$则实数x的取值范围是( )
| A. | (-1,0) | B. | [-1,0] | C. | (-∞,-1)∪(0,+∞) | D. | (-∞,-1]∪[0,+∞) |
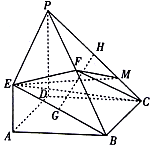 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.