题目内容
2．已知F1，F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0．b＞0）的左、右焦点，其离心率为e，点B的坐标为（0，b），直线F1B与双曲线C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴，直线F1B的交点分别为M，R，若△RMF1与△PQF2的面积比为e，则e的值为？分析 分别求出P，Q，M的坐标，利用△RMF1与△PQF2的面积之比为e，|MF2|=|F1F2|=2c，可得3c=xM=$\frac{{c}^{3}}{{c}^{2}-{a}^{2}}$，即可得出结论．
解答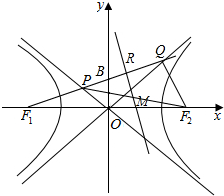 
解：由题意，|OB|=b，|OF1|=c．∴kPQ=$\frac{b}{c}$，kMN=-$\frac{c}{b}$．
直线PQ为：y=$\frac{b}{c}$（x+c），与y=$\frac{b}{a}$x．联立得：Q（$\frac{ac}{c-a}$，$\frac{bc}{c-a}$）；
与y=-$\frac{b}{a}$x．联立得：P（$\frac{-ac}{c+a}$，$\frac{bc}{c+a}$）．
直线MN为：y-$\frac{bc}{c+a}$=-$\frac{c}{b}$（x-$\frac{-ac}{c+a}$），
令y=0得：xM=$\frac{{c}^{3}}{{c}^{2}-{a}^{2}}$
又△RMF1与△PQF2的面积之比为e，∴|MF2|=|F1F2|=2c，∴3c=xM=$\frac{{c}^{3}}{{c}^{2}-{a}^{2}}$，
解之得：e2=$\frac{3}{2}$，
∴e=$\frac{\sqrt{6}}{2}$．
点评 本题考查双曲线的方程与性质，考查学生的计算能力，属于中档题．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
12．
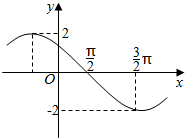已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）
已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）| A． | f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{4}$） | B． | f（x）=2sin（$\frac{1}{2}$x+$\frac{3π}{4}$） | C． | f（x）=2sin（2x-$\frac{π}{4}$） | D． | f（x）=2sin（2x+$\frac{3π}{4}$） |
13．函数$y=cos（-x）cos（\frac{π}{2}-x）$的最小正周期是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |