题目内容
10.已知抛物线y2=4x上的任意一点P,记点P到y轴的距离为d,对于给定点A(4,5),则|PA|+d的最小值为$\sqrt{34}$-1.分析 抛物线y2=4x的焦点F(1,0),准线l:x=-1,过点P作PN⊥l交y轴于点M,垂足为N,则|PF|=|PN|,|PA|+d≥|AF|-1.即可得出.
解答 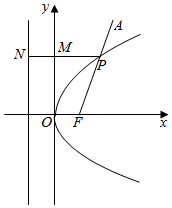 解:抛物线y2=4x的焦点F(1,0),准线l:x=-1.
解:抛物线y2=4x的焦点F(1,0),准线l:x=-1.
如图所示,过点P作PN⊥l交y轴于点M,垂足为N,
则|PF|=|PN|,
∴d=|PF|-1,
∴|PA|+d≥|AF|-1=$\sqrt{(4-1)^{2}+{5}^{2}}$-1=$\sqrt{34}$-1.
当且仅当A,P,F三点共线时,取得最小值$\sqrt{34}$-1.
故答案为:$\sqrt{34}$-1.
点评 本题考查了抛物线的定义及其标准方程、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知空间中四个不共面的点O、A、B、C,若|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,且cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=cos<$\overrightarrow{OA}$,$\overrightarrow{OC}$>,则sin<$\overrightarrow{OA}$,$\overrightarrow{BC}$>的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
1.将函数y=sinx的图象向左平移φ(0≤φ≤2π)个单位后,得到函数$y=sin(x-\frac{π}{6})$的图象,则φ=( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{7π}{6}$ | D. | $\frac{11π}{6}$ |
15.命题“若x<3,则x2≤9”的逆否命题是( )
| A. | 若x≥3,则x2>9 | B. | 若x2≤9,则x<3 | C. | 若x2>9,则x≥3 | D. | 若x2≥9,则x>3 |
20.下列各角中,是第一象限角的是( )
| A. | 1200° | B. | -1140° | C. | -1350° | D. | 1850° |
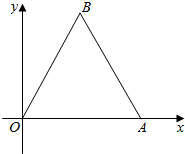 正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.
正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.