题目内容
20.已知曲线f(x)=x3+x2+x+3在x=-1处的切线与抛物线y=2px2相切,则抛物线的准线方程为( )| A. | $x=\frac{1}{16}$ | B. | x=1 | C. | y=-1 | D. | y=1 |
分析 求出f(x)的导数,求得x=-1处切线的斜率,以及切点,运用点斜式方程可得切线的方程,联立抛物线方程,运用相切的条件:判别式为0,解得p,进而得到抛物线的方程和准线方程.
解答 解:f(x)=x3+x2+x+3的导数为f′(x)=3x2+2x+1,
则在x=-1处的切线斜率为3-2+1=2.切点为(-1,2),
切线的方程为y-2=2(x+1),即y=2x+4,
与抛物线y=2px2相切,可得2px2-2x-4=0,
由判别式△=4+32p=0,
解得p=-$\frac{1}{8}$.
抛物线的方程为y=-$\frac{1}{4}$x2,
即x2=-4y,
即有准线方程为y=1.
故选:D.
点评 本题考查导数的运用:求切线的方程,考查直线和抛物线相切的条件:判别式为0,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
10.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈(-∞,2]}\\{lo{g}_{2}x,x∈(2,+∞)}\end{array}\right.$,则满足f(x)=3的x的值是( )
| A. | log23 | B. | 8 | C. | log23或8 | D. | 8或6 |
11.设i是虚数单位,复数z=(1-2i)(i+4),则|z|=( )
| A. | $\sqrt{65}$ | B. | 5$\sqrt{3}$ | C. | $\sqrt{85}$ | D. | $\sqrt{95}$ |
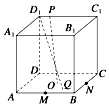 在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC的中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足$\overrightarrow{MQ}$=λ$\overrightarrow{MN}$的实数λ有2个.
在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC的中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足$\overrightarrow{MQ}$=λ$\overrightarrow{MN}$的实数λ有2个.