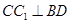题目内容
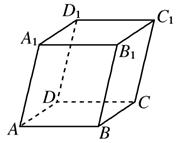
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都为1,且两两夹角为60°.
(1)求AC1的长;
(2)求BD1与AC夹角的余弦值.
设![]() =a,
=a,![]() =b,
=b,![]() =c,则|a|=|b|=|c|=1,
=c,则|a|=|b|=|c|=1,
〈a,b〉=〈b,c〉=〈c,a〉=60°,
∴a·b=b·c=c·a=![]() .
.
(1)|![]() |2=(a+b+c)2
|2=(a+b+c)2
=a2+b2+c2+2a·b+2b·c+2a·c
=1+1+1+2×(![]() +
+![]() +
+![]() )=6.
)=6.
∴AC1=|![]() |=
|=![]() .
.
(2)![]() =b+c-a,
=b+c-a,![]() =a+b.
=a+b.
∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() .
.
![]() ·
·![]() =(b+c-a)·(a+b)
=(b+c-a)·(a+b)
=b2-a2+a·c+b·c=1.
∴cos〈![]() ,
,![]() 〉=
〉=![]() .
.
∴AC与BD1夹角的余弦值为![]() .
.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
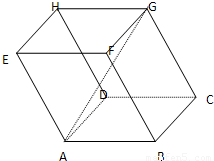
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.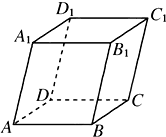 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,