题目内容
2．函数y=$\frac{x-cosx}{x+sinx}$在x=2处的导数是$\frac{3sin2+1-cos2}{（2+sin2）^{2}}$．分析 求导y′=$\frac{（x-cosx）′（x+sinx）-（x-cosx）（x+sinx）^{′}}{（x+sinx）^{2}}$=$\frac{（1+sinx）（x+sinx）-（x-cosx）（1+cosx）}{（x+sinx）^{2}}$，代入x=2化简即可．
解答 解：y′=$\frac{（x-cosx）′（x+sinx）-（x-cosx）（x+sinx）^{′}}{（x+sinx）^{2}}$
=$\frac{（1+sinx）（x+sinx）-（x-cosx）（1+cosx）}{（x+sinx）^{2}}$
=$\frac{sinx+xsinx+1-xcosx+cosx}{（x+sinx）^{2}}$，
故y′|x=2=$\frac{3sin2+1-cos2}{（2+sin2）^{2}}$，
故答案为：$\frac{3sin2+1-cos2}{（2+sin2）^{2}}$．
点评 本题考查了导数的运算及学生的化简运算能力．
练习册系列答案
相关题目
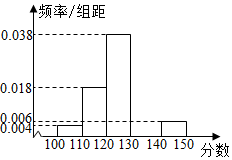2015-2016学年高二A班50名学生在其中数学测试中（满分150分），成绩都介于100分到150分之间，将测试结果按如下方式分成五组，第一组[100，110），第二组[110，120），…，第五组[140，150），按上述分组方法得到的频率分布直方图如图所示，
10．设圆（x-a）2+（y-2）2=4的圆心在直线x-y+3=0上，则a的值为（ ）
| A． | 1 | B． | -1 | C． | 5 | D． | -5 |
17．下列直线中，平行于直线x-y+1=0且与圆x2+y2=4相切的是（ ）
| A． | x+y-2=0 | B． | x+y+2$\sqrt{2}$=0 | C． | x-y-2=0 | D． | x-y-2$\sqrt{2}$=0 |