题目内容
17.对于R上可导的函数f(x),若a>b>1,且有(x-1)f′(x)>0则必有( )| A. | f(a)+f(b)<2f(1) | B. | f(a)+f(b)≤2f(1) | C. | f(a)+f(b)≥2f(1) | D. | f(a)+f(b)>2f(1) |
分析 由不等式,得出f(x)的单调性,由单调性,得出f(a),f(b),f(1)的大小.
解答 解:由(x-1)f′(x)>0知
$\left\{\begin{array}{l}{x-1>0}\\{f′(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x-1<0}\\{f′(x)<0}\end{array}\right.$
∴x>1时,f(x)单调递增
x<1时,f(x)单调递减,
∵a>b>1
∴f(a)>f(b)>f(1)
∴f(a)+f(b)>2f(1)
故选D
点评 本题考查不等式的理解,由f(x)的单调性,可得出选项.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
7.已知函数f(x)由下表给出,则f(2)=3.
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
5.若x>0,则函数f(x)=4x+$\frac{2}{x}$的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
6.将由曲线y=cosx,直线x=0,x=π,y=0所围成图形的面积写成定积分的形式为( )
| A. | ${∫}_{0}^{π}$cosxdx | B. | ${∫}_{0}^{\frac{π}{2}}$cosxdx+|${∫}_{\frac{π}{2}}^{π}$cosxdx| | ||
| C. | ${∫}_{0}^{π}$2sinxdx | D. | ${∫}_{0}^{π}$2|cosx|dx |
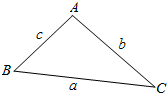 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.