题目内容
7.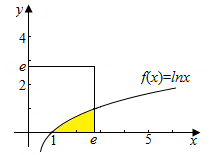 如图所示,若在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落在阴影部分的概率为$\frac{1}{e^2}$.
如图所示,若在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落在阴影部分的概率为$\frac{1}{e^2}$.
分析 根据几何概型的概率公式结合积分的应用求出对应区域的面积,进行求解即可.
解答  解:由图可知正方形关于直线y=x对称,又y=ex与y=lnx图象也关于直线y=x对称,
解:由图可知正方形关于直线y=x对称,又y=ex与y=lnx图象也关于直线y=x对称,
如下图,则$\int_1^e{{{({lnx})}_{\;}}}dx={\int_0^1{({e-{e^x}})}_{\;}}dx=1$,正方形面积为e2,则概率为$\frac{1}{e^2}$,故答案为:$\frac{1}{e^2}$.
点评 本题主要考查几何概型的概率的计算,遇到较难的指数或对数函数问题,可以先联系反函数,被积函数为对数函数时不好求,可根据图象特征等价转化为指数函数.

练习册系列答案
相关题目
18.执行如图所示的程序框图,则输出的k的值是( )


| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
2.把一枚质地均匀的硬币连续抛2次,出现正、反面交替的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |