题目内容
19.设等差数列{an}的前n项和为Sn,且S5=5S2,2a1+1=a3.(1)求数列{an}的通项公式;
(2)设数列bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,求{bn}的前n项和Tn.
分析 (1)通过联立S5=5S2、2a1+1=a3,计算可知a1=d=1,进而计算可得结论;
(2)通过(1)裂项可知bn=$\frac{1}{n}$-$\frac{1}{n+1}$,进而并项相加即得结论.
解答 解:(1)设等差数列{an}的公差为d,
∵S5=5S2,2a1+1=a3,
∴5a1+10d=5(2a1+d),2a1+1=a1+2d,
整理得:a1=d=1,
∴数列{an}的通项公式an=n;
(2)由(1)可知bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴Tn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14.已知x,y的取值如表:
若依据表中数据所画的散点图中,所有样本点(xi,yi)(i=1,2,3,4,5)都在曲线y=$\frac{1}{2}$x2+a附近波动,则a=1.
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 1.3 | 3.2 | 5.6 | 8.9 |
9.已知集合M={x|3x-x2>0},N={x|x2-4x+3>0},则M∩N=( )
| A. | (0,1) | B. | (1,3) | C. | (0,3) | D. | (3,+∞) |
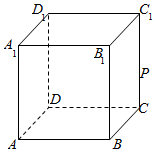 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.