题目内容
(本小题满分10分)在平面直角坐标系xOy中,已知抛物  的准线方程为
的准线方程为  过点M(0,-2)作抛物线的切线MA,切点为A(异于点O).直线
过点M(0,-2)作抛物线的切线MA,切点为A(异于点O).直线 过点M与抛物线交于两点B,C,与直线OA交于点N.
过点M与抛物线交于两点B,C,与直线OA交于点N.

(1)求抛物线的方程;
(2)试问:  的值是否为定值?若是,求出定值;若不是,说明理由。
的值是否为定值?若是,求出定值;若不是,说明理由。
(1) (2)2.
(2)2.
【解析】
试题分析:(1)由抛物线准线性质得 ,所以抛物线的方程为
,所以抛物线的方程为 ,(2)先利用导数求切点坐标:
,(2)先利用导数求切点坐标: 设
设 ,
, 解得
解得 ,所以直线
,所以直线 的方程为
的方程为 .再根据直线与抛物线联立方程组,用直线斜率表示B,C坐标关系:
.再根据直线与抛物线联立方程组,用直线斜率表示B,C坐标关系: ,
,
所以
试题解析:(1)由题设知, ,即
,即
所以抛物线的方程为 2分
2分
(2)因为函数 的导函数为
的导函数为 ,设
,设 ,
,
则直线 的方程为
的方程为 , 4分
, 4分
因为点 在直线
在直线 上,所以
上,所以 .
.
联立 解得
解得 . 5分
. 5分
所以直线 的方程为
的方程为 . 6分
. 6分
设直线 方程为
方程为 ,
,
由 ,得
,得 ,
,
所以 . 7分
. 7分
由 ,得
,得 . 8分
. 8分
所以 ,
,
故 为定值2. 10分
为定值2. 10分
考点:直线与抛物线位置关系

练习册系列答案
相关题目
(本小题满分13分)最近,张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案,且一年后投资盈亏的情况如下:
(1)投资股市:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概 率 |
|
|
|
(2)购买基金:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概 率 |
|
|
|
(Ⅰ)当 时,求q的值;
时,求q的值;
(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求 的取值范围;
的取值范围;
(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
 年
年 月,某市进行了“居民幸福度”的调查,某师大附中学生会组织部分同学,用“
月,某市进行了“居民幸福度”的调查,某师大附中学生会组织部分同学,用“ 分制”随机调查“狮子山”社区人们的幸福度.现从调查人群中随机抽取
分制”随机调查“狮子山”社区人们的幸福度.现从调查人群中随机抽取 名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
 分,则称该人的幸福度为“极幸福”,求从这
分,则称该人的幸福度为“极幸福”,求从这 人中随机选取
人中随机选取 人,至
人,至 人是“极幸福”的概率;
人是“极幸福”的概率; 人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选
人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选 人,记
人,记
 的分布列及数学期望.
的分布列及数学期望. 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,若
,若 ,且
,且 ,则下列关系一定不成立的是( )
,则下列关系一定不成立的是( ) B.
B. C.
C. D.
D.
 与直线
与直线  互相平行,则2a+3b的最小值为________.
互相平行,则2a+3b的最小值为________.
 0是△ABC的外接圆,AB = AC,延长BC到点D,使得CD = AC,连结AD交
0是△ABC的外接圆,AB = AC,延长BC到点D,使得CD = AC,连结AD交 O于点E.求证:BE平分
O于点E.求证:BE平分 ABC
ABC
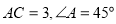 ,点D满足
,点D满足 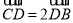 ,且
,且 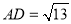 ,则BC的长为_______ .
,则BC的长为_______ . 中,
中, ,
, 、
、 分别是
分别是 ,
, 的中点.
的中点.
 ∥平面
∥平面 ;
; 平面
平面 ;
; ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.




