题目内容
(本小题满分14分)如图,在直三棱柱 中,
中, ,
, 、
、 分别是
分别是 ,
, 的中点.
的中点.

(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(1)证明详见解析;(2)证明详见解析;(3) .
.
【解析】
试题分析:本题以直三棱柱为几何背景,考查线线垂直、线面垂直、面面垂直、线线平行、线面平行、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力、转化能力、计算能力. 第一问,先利用 中,EF为中位线,得出
中,EF为中位线,得出 ,再利用线面平行的判定得
,再利用线面平行的判定得 平面
平面 ;第二问,结合第一问
;第二问,结合第一问 ,而利用
,而利用 平面
平面 线面垂直的性质,可得
线面垂直的性质,可得 ,由于
,由于 ,所以得
,所以得 ,所以利用线面垂直的判定得
,所以利用线面垂直的判定得 平面
平面 ,最后利用面面垂直的判定得平面
,最后利用面面垂直的判定得平面 平面
平面 ;第三问,利用等体积转化法将
;第三问,利用等体积转化法将 转化为
转化为 ,再计算体积.
,再计算体积.
试题解析:(1)连结 ,∵直三棱柱
,∵直三棱柱 中,四边形
中,四边形 是矩形,
是矩形,
∴点 在
在 上,且
上,且 为
为 的中点.
的中点.
在 中,∵ E,F分别是
中,∵ E,F分别是 ,
, 的中点, 故
的中点, 故 . 2分
. 2分
又∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 4分
4分
(2)在直三棱柱 中,
中, 平面
平面 ,∴
,∴ 6分
6分
由(1)知 ,且
,且 ,则
,则
∵ ,∴
,∴ 平面
平面 9分
9分
又∵ 平面
平面 ,∴平面
,∴平面 平面
平面 10分
10分
(3) 12分
12分
 14分
14分
考点:线线垂直、线面垂直、面面垂直、线线平行、线面平行、三棱锥的体积.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 的正方体的俯视图是一个面积为
的正方体的俯视图是一个面积为 的正方形,则该正方体的正视图的面积不可能等于( )
的正方形,则该正方体的正视图的面积不可能等于( ) B.
B. C.
C. D.
D.
 的准线方程为
的准线方程为  过点M(0,-2)作抛物线的切线MA,切点为A(异于点O).直线
过点M(0,-2)作抛物线的切线MA,切点为A(异于点O).直线 过点M与抛物线交于两点B,C,与直线OA交于点N.
过点M与抛物线交于两点B,C,与直线OA交于点N.
 的值是否为定值?若是,求出定值;若不是,说明理由。
的值是否为定值?若是,求出定值;若不是,说明理由。 满足
满足 ,则
,则 的最小值为_______.
的最小值为_______. (i是虚数单位),则z的虚部为_______.
(i是虚数单位),则z的虚部为_______. 是平面内不共线的三点,点
是平面内不共线的三点,点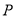 在该平面内且有
在该平面内且有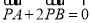 ,现将一粒黄豆随机
,现将一粒黄豆随机 内,则这粒黄豆落在
内,则这粒黄豆落在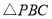 内的概率为___________.
内的概率为___________. 与圆
与圆 的位置关系为( )
的位置关系为( ) ,
, ,
, ,若
,若 ,则实数
,则实数 ______.
______. ,则
,则 _____.
_____.