题目内容
11.设函数f(x)=lnx+$\frac{m}{x}$,m∈R(1)当m=e(e为自然对数的底数)时,f(x)的极小值;
(2)若函数g(x)=f′(x)-$\frac{x}{3}$存在唯一零点,求m的范围.
分析 (1)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出f(x)的极小值即可;
(2)令g(x)=0,得m=-$\frac{1}{3}$x3+x(x>0),设φ(x)=-$\frac{1}{3}$x3+x(x≥0),根据函数的单调性画出函数φ(x)的草图,求出m的范围即可.
解答 解 (1)由题设,当m=e时,f(x)=ln x+$\frac{e}{x}$,
则f′(x)=$\frac{x-e}{x2}$,由f′(x)=0,得x=e.
∴当x∈(0,e),f′(x)<0,f(x)在(0,e)上单调递减,
当x∈(e,+∞),f′(x)>0,f(x)在(e,+∞)上单调递增,
∴当x=e时,f(x)取得极小值f(e)=ln e+$\frac{e}{e}$=2,
∴f(x)的极小值为2…(4分)
(2)由题设g(x)=f′(x)-$\frac{x}{3}$=$\frac{1}{x}$-$\frac{m}{x2}$-$\frac{x}{3}$(x>0),
令g(x)=0,得m=-$\frac{1}{3}$x3+x(x>0).
设φ(x)=-$\frac{1}{3}$x3+x(x≥0),
则φ′=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
∴x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是φ(x)的最大值点.
∴φ(x)的最大值为φ(1)=$\frac{2}{3}$.
又φ(0)=0,结合y=φ(x)的图象(如图),
可知
当m=$\frac{2}{3}$时,函数g(x)有且只有一个零点;
当m≤0时,函数g(x)有且只有一个零点.
所以,当m=$\frac{2}{3}$或m≤0时,函数g(x)有且只有一个零点;…(12分)
点评 本题考查了函数的单调性、最值、极值问题,考查导数的应用以及数形结合思想,转化思想,是一道中档题.

 阅读快车系列答案
阅读快车系列答案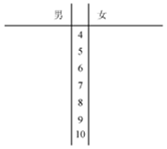 某学校对男女学生进行有关“习惯与礼仪”的调查,分别随机抽查了18名学生进行评分(百分制:得分越高,习惯与礼仪越好),评分记录如下:
某学校对男女学生进行有关“习惯与礼仪”的调查,分别随机抽查了18名学生进行评分(百分制:得分越高,习惯与礼仪越好),评分记录如下:男生:44,46,46,52,54,55,56,57,58,58,63,66,70,73,75,85,90,94.
女生:51,52,55,58,63,63,65,69,69,70,74,78,77,77,83,83,89,100
(1)请用茎叶图表示上面的数据,并通过茎叶图比较男女生“习惯与礼仪”评分的平均值及分散程度(不要求计算出具体的值,给出结论即可).
(2)记评分在60分以下的等级为较差,评分在60分以上的等级为较好,请完成2×2列联表,并判断是否有95%的把握认为“习惯与礼仪”与性别有关?并说明理由.
| 等级 性别 | 较差 | 较好 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 | K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ |
| k | 3.841 | 6.635 | 10.828 |
| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
(2)请估计该市一面积为120m2的新电梯房的房价.
| A. | 24 | B. | $\frac{49}{2}$ | C. | 25 | D. | $\frac{324}{13}$ |
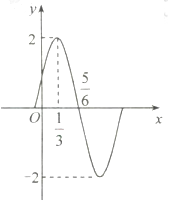 已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.
已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.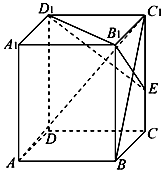 在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.