题目内容
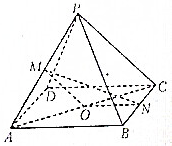如图，在四棱锥P-ABCD中，M、N分别是侧棱PA和底面BC边的中点，O是底面?ABCD对角线AC的中点，求证：过O、M、N三点的平面与侧面PCD平行．考点：平面与平面垂直的判定
专题：推理和证明
分析：利用三角形的中位线定理易证MO
PC，ON
AB，再由线面平行的判定定理证得MO∥平面PCD，ON∥平面PCD，最后利用面面平行的判定定理即可证得结论成立．
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
解答：
证明：∵M、O分别为PA和底面AC边的中点，
∴MO是△PAO的中位线，
∴MO
PC，
又MO?平面PCD，PC?平面PCD，
∴MO∥平面PCD；①
又N是底面BC边的中点，ON是△ABO的中位线，ON
AB，底面ABCD为平行四边形，AB
CD，
∴ON
CD，同理可证，ON∥平面PCD；②
又OM∩ON=O，OM?平面OMN，ON?平面OMN，③
由①②③得：平面OMN∥平面PCD（面面平行的判定定理）．
∴MO是△PAO的中位线，
∴MO
| ∥ |
. |
| 1 |
| 2 |
又MO?平面PCD，PC?平面PCD，
∴MO∥平面PCD；①
又N是底面BC边的中点，ON是△ABO的中位线，ON
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴ON
| ∥ |
. |
| 1 |
| 2 |
又OM∩ON=O，OM?平面OMN，ON?平面OMN，③
由①②③得：平面OMN∥平面PCD（面面平行的判定定理）．
点评：本题考查平面与平面平行的判定，考查三角形的中位线定理与线面平行的判定定理、面面平行的判定定理，考查推理能力，考查转化思想．
练习册系列答案
相关题目
函数f（x）=
的定义域为（ ）
| 1 |
| x-2 |
| A、（-∞，2） |
| B、（2，+∞） |
| C、（-∞，0）∪（0，+∞） |
| D、（-∞，2）∪（2，+∞） |
已知全集U={0，1，2，3，4}且∁UA={0，2}，则集合A的非空真子集共有（ ）
| A、5个 | B、6个 | C、7个 | D、8个 |
已知函数y=f（x-1）的定义域为[1，3]，则函数y=f（log3x）的定义域为（ ）
| A、[1，9] |
| B、[0，1] |
| C、[0，2] |
| D、[0，9] |
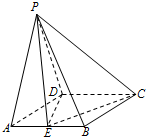在四棱锥P-ABCD中，底面是边长为2的菱形，∠BAD=60°，PA=PD=3，PD⊥CD．E为AB中点．
如图所示，在直三棱柱ABC-A1B1C1中，底面是等腰三角形，∠ACB=90°，侧棱AA1=2，CA=2，D是CC1的中点，试问在线段A1B上是否存在一点E（不与端点重合），使得点A1到平面AED的距离为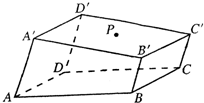
如图所示的一块木料中，棱BC平行于面A′C′．