题目内容
已知数列{an}的前n项和满足an+1=
Sn,且a1=
(n∈N*)
(1)求数列{an}的通项公式;
(2)bn=nan,求数列{bn}的前n项和Tn.
| 1 |
| 3 |
| 1 |
| 4 |
(1)求数列{an}的通项公式;
(2)bn=nan,求数列{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用地推关系证明数列是等比数列,然后求出等比数列的通项公式.
(2)先构造数列然后利用乘公比错位相减法求数列的和,进一步求出结果.
(2)先构造数列然后利用乘公比错位相减法求数列的和,进一步求出结果.
解答:
解:(1)已知an+1=
Sn①
则:an=
Sn-1②
①-②得:an+1-an=
an
整理得:
=
(常数)
所以:{an}是以a1=
为首项
为公比的等比数列.
an=
(
)n-1
(2)由(1)得:an=
(
)n-1
则:bn=nan=
(
)n-1=
[n•(
)n-1]
设cn=n•(
)n-1
则Sn=c1+c2+…+cn=1•(
)0+2•(
)1+…+n•(
)n-1③
Sn=1•(
)1+2(
)2+…+n•(
)n④
所以:③-④得:
(1-
)Sn=Sn=
-n•(
)n
解得:Sn=9+(3n-9)(
)n
所以:Tn=b1+b2+…+bn=
Sn=
+
| 1 |
| 3 |
则:an=
| 1 |
| 3 |
①-②得:an+1-an=
| 1 |
| 3 |
整理得:
| an+1 |
| an |
| 4 |
| 3 |
所以:{an}是以a1=
| 1 |
| 4 |
| 4 |
| 3 |
an=
| 1 |
| 4 |
| 4 |
| 3 |
(2)由(1)得:an=
| 1 |
| 4 |
| 4 |
| 3 |
则:bn=nan=
| n |
| 4 |
| 4 |
| 3 |
| 1 |
| 4 |
| 4 |
| 3 |
设cn=n•(
| 4 |
| 3 |
则Sn=c1+c2+…+cn=1•(
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
所以:③-④得:
(1-
| 4 |
| 3 |
1-(
| ||
1-
|
| 4 |
| 3 |
解得:Sn=9+(3n-9)(
| 4 |
| 3 |
所以:Tn=b1+b2+…+bn=
| 1 |
| 4 |
| 9 |
| 4 |
(3n-9)(
| ||
| 4 |
点评:本题考查的知识要点:利用递推关系式求数列的通项公式,构造新数列然后利用错位相减法求数列的和.属于基础题型.

练习册系列答案
相关题目
下列集合表示方法正确的是( )
| A、{1,3,3} |
| B、{全体实数} |
| C、{2,4} |
| D、不等式x2-1>2的解集是{x2-1>0} |
下列说法不正确的是( )
| A、0∈N | ||
| B、-5∈Z | ||
| C、π∈Q | ||
D、-
|
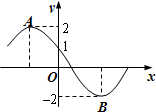 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,