题目内容
在△ABC中,
=
,
=
.设BF,CE交于点P,且
=λ
,
=μ
(λ,μ∈R),则λ+μ的值为 .
| AE |
| 1 |
| 3 |
| AB |
| AF |
| 2 |
| 3 |
| AC |
| EP |
| EC |
| FP |
| FB |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由已知可得E为线段AB上靠近A的三等分点,F为线段AC上靠近C的三等分点,进而根据
=λ
,
=μ
,可得
=(1-λ)
+λ
=
(1-λ)
+λ
=μ
+(1-μ)
=μ
+
(1-μ)
,进而由平面向量的基本定理可得关于λ和μ的方程组,解方程组可得λ+μ的值.
| EP |
| EC |
| FP |
| FB |
| AP |
| AE |
| AC |
| 1 |
| 3 |
| AB |
| AC |
| AB |
| AF |
| AB |
| 2 |
| 3 |
| AC |
解答:
解:∵在△ABC中,
=
,
=
.
∴E为线段AB上靠近A的三等分点,F为线段AC上靠近C的三等分点,如下图所示:
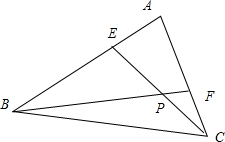
∴
=
+
=
-
,
=
+
=-
+
,
∵
=λ
,
=μ
∴
=(1-λ)
+λ
=
(1-λ)
+λ
,
且
=μ
+(1-μ)
=μ
+
(1-μ)
,
根据平面向量的基本定理可得:
,
解得:
,
∴λ+μ=
,
故答案为:
| AE |
| 1 |
| 3 |
| AB |
| AF |
| 2 |
| 3 |
| AC |
∴E为线段AB上靠近A的三等分点,F为线段AC上靠近C的三等分点,如下图所示:

∴
| CE |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
| 1 |
| 3 |
| AB |
| AC |
| BF |
| 2 |
| 3 |
| BC |
| 1 |
| 3 |
| BA |
| AB |
| 2 |
| 3 |
| AC |
∵
| EP |
| EC |
| FP |
| FB |
∴
| AP |
| AE |
| AC |
| 1 |
| 3 |
| AB |
| AC |
且
| AP |
| AB |
| AF |
| AB |
| 2 |
| 3 |
| AC |
根据平面向量的基本定理可得:
|
解得:
|
∴λ+μ=
| 5 |
| 7 |
故答案为:
| 5 |
| 7 |
点评:本题考查的知识点是平面向量的基本定理,其中根据已知得到
=(1-λ)
+λ
=
(1-λ)
+λ
=μ
+(1-μ)
=μ
+
(1-μ)
,是解答的关键.
| AP |
| AE |
| AC |
| 1 |
| 3 |
| AB |
| AC |
| AB |
| AF |
| AB |
| 2 |
| 3 |
| AC |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中,为假命题的是( )
| A、?x∈R,lnx=1 |
| B、?x∈R,sinx=1 |
| C、?x∈R,x2>0 |
| D、?x∈R,ex>0 |
设a=(
)x,b=(
)x-1,c=log
x,若x>1,则a,b,c的大小关系是( )
| 3 |
| 4 |
| 4 |
| 3 |
| 3 |
| 4 |
| A、a<b<c |
| B、b<a<c |
| C、c<a<b |
| D、b<c<a |