题目内容
2.设f(x)=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}-lnx-\frac{1}{2},x>0}\\{x+\frac{1}{x}+1,x<0}\end{array}\right.$,若方程[f(x)]2+af(x)+b=0(a>0)有四个不相等的实根,则$\frac{b+1}{a+2}$的取值范围是(-∞,$\frac{1}{3}$)∪($\frac{1}{2}$,+∞).分析 分类讨论,从而确定函数的单调性及值域,从而化为方程x2+ax+b=0(a>0)有两个不同的实根,且在(-∞,-1)∪(0,+∞)上;从而利用线性规划求解即可.
解答 解:①当x>0时,f(x)=$\frac{1}{2}$x2-lnx-$\frac{1}{2}$,
f′(x)=x-$\frac{1}{x}$,
故f(x)在(0,1]上单调递减,在(1,+∞)上单调递增;
而f(1)=0,故f(x)∈[0,+∞);
②当x<0时,f(x)=x+$\frac{1}{x}$+1,
故f(x)在(-1,0)上单调递减,在(-1,+∞)上单调递增;
且f(-1)=-1;故f(x)∈(-∞,-1];
∵方程[f(x)]2+af(x)+b=0(a>0)有四个不相等的实根,
∴方程x2+ax+b=0(a>0)有两个不同的实根,
且在(-∞,-1)∪(0,+∞)上;
若两个不同的实根在(-∞,-1)上,
则$\left\{\begin{array}{l}{a>0}\\{△={a}^{2}-4b>0}\\{-\frac{a}{2}<-1}\\{1-a+b>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a>2}\\{1-a+b>0}\\{{a}^{2}-4b>0}\end{array}\right.$,
作平面区域如下,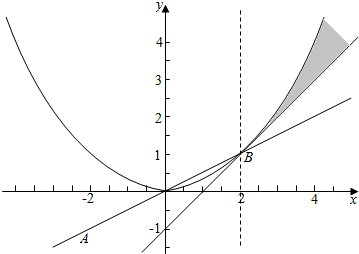 ,
,
$\frac{b+1}{a+2}$的几何意义是阴影内的点与点A(-2,-1)连线的斜率,
而kAB=$\frac{1+1}{2+2}$=$\frac{1}{2}$,
故$\frac{b+1}{a+2}$>$\frac{1}{2}$;
若两个不同的实根分别在(-∞,-1)与(0,+∞)上,
则$\left\{\begin{array}{l}{a>0}\\{1-a+b<0}\\{b<0}\end{array}\right.$,
作平面区域如下,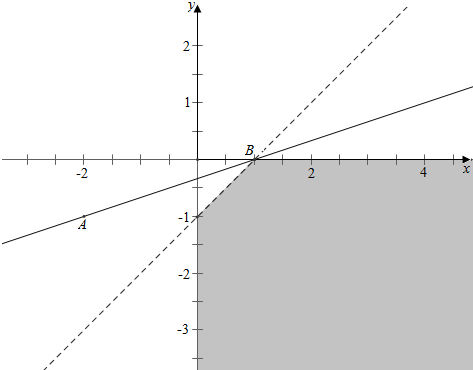
$\frac{b+1}{a+2}$的几何意义是阴影内的点与点A(-2,-1)连线的斜率,
而kAB=$\frac{0+1}{1+2}$=$\frac{1}{3}$,
故$\frac{b+1}{a+2}$<$\frac{1}{3}$;
∵a>0,∴两个不同的实根不可能同时在(0,+∞)上,
综上所述,
$\frac{b+1}{a+2}$的取值范围是(-∞,$\frac{1}{3}$)∪($\frac{1}{2}$,+∞).
故答案为:(-∞,$\frac{1}{3}$)∪($\frac{1}{2}$,+∞).
点评 本题考查了数形结合的思想应用及分类讨论的思想应用,同时考查了导数的综合应用.

| A. | 旋转双曲面 | B. | 旋转椭球面 | C. | 旋转抛物面 | D. | 椭圆抛物面 |
| A. | $\frac{|a|}{\sqrt{1+{a}^{2}}}$ | B. | $\frac{a}{\sqrt{1+{a}^{2}}}$ | C. | -$\frac{a}{\sqrt{1+{a}^{2}}}$ | D. | -$\frac{1}{\sqrt{1+{a}^{2}}}$ |
 如图,将一个边长为2cm和5cm,两邻边夹角为60°的平行四边形绕其5cm边上的高所在直线旋转一周形成的几何体是圆台.
如图,将一个边长为2cm和5cm,两邻边夹角为60°的平行四边形绕其5cm边上的高所在直线旋转一周形成的几何体是圆台.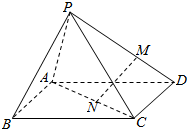 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.