题目内容
【题目】已知高为3的正三棱柱
的每个顶点都在球
的表面上，若球的表面积为
，则异面直线
与
所成角的余弦值为
A. 
B. 
C. 
D. 
【答案】B
【解析】
由三棱柱外接球的表面积得：三棱柱的底面边长为a，则此三棱柱的外接球的半径
，又由
，所以
，得：
，由异面直线平面角的作法得：分别取BC、
、
的中点E、F、G，连接GF、EF、EG，因为
，
，则
或其补角
为异面直线
与
所成角，再利用余弦定理求解即可．
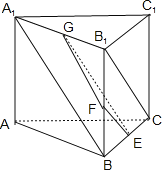
设三棱柱的底面边长为a，则此三棱柱的外接球的半径，
又由已知有，
所以，
联立
得：，
分别取BC、、的中点E、F、G，
连接GF、EF、EG，
因为，，
则或其补角为异面直线与所成角，
又易得：
，
，
在
中，由余弦定理得：
，又
为锐角
即异面直线与所成角的余弦值为
，
故选：B．
练习册系列答案
相关题目
