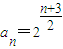题目内容
已知双曲线an-1y2-anx2=an-1an的一个焦点为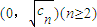 ,且c1=6,一条渐近线方程为
,且c1=6,一条渐近线方程为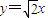 ,其中{an}是以4为首项的正数数列,记Tn=a1c1+a2c2+…+ancn(n∈N*).
,其中{an}是以4为首项的正数数列,记Tn=a1c1+a2c2+…+ancn(n∈N*).(1)求数列{cn}的通项公式;
(2)数列{cn}的前n项和为Sn,求
 ;
;(3)若不等式
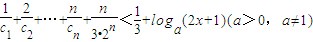 对一切自然数n(n∈N*)恒成立,求实数x的取值范围.
对一切自然数n(n∈N*)恒成立,求实数x的取值范围.
【答案】分析:(1)由双曲线方程得:Cn=an+an+1,由一条渐进线方程为  和an是以4为首项的正项数列得到an的通项公式化简,进而推出数列Cn的通项公式;
和an是以4为首项的正项数列得到an的通项公式化简,进而推出数列Cn的通项公式;
(2)分别计算Tn=a1c1+a2c2+…+ancn(n∈N*),Sn,再求 ;
;
(3)先把Cn的通项公式代入到不等式左边,错位相减得 ,把S代入到不等式左边得到要使不等式对一切自然数n恒成立
,把S代入到不等式左边得到要使不等式对一切自然数n恒成立  ,即要loga(2x+1)≥0,讨论a的取值得到x的范围.
,即要loga(2x+1)≥0,讨论a的取值得到x的范围.
解答:解:(1)由双曲线方程得:Cn=an+an+1,又因为一条渐近线 .
.
∴ ,∴an=4•2n+1=2n+1
,∴an=4•2n+1=2n+1
∴Cn=3•2n
(2)Sn=6(2n-1),Tn=8(22n-1),∴
(3)令S= +
+ +…+
+…+ =
= +
+ +…+
+…+
由错位相减得
故原不等式 恒成立
恒成立
∴loga(2x+1)≥0
(i)当a>1时,2x+1≥1⇒x≥0
(ii)当
∴
点评:本题以双曲线为载体,考查考查学生灵活运用等比数列的通项公式,以及掌握双曲线的简单性质,理解不等式恒成立时取到的条件,掌握对数函数的图象与性质.
 和an是以4为首项的正项数列得到an的通项公式化简,进而推出数列Cn的通项公式;
和an是以4为首项的正项数列得到an的通项公式化简,进而推出数列Cn的通项公式;(2)分别计算Tn=a1c1+a2c2+…+ancn(n∈N*),Sn,再求
 ;
;(3)先把Cn的通项公式代入到不等式左边,错位相减得
 ,把S代入到不等式左边得到要使不等式对一切自然数n恒成立
,把S代入到不等式左边得到要使不等式对一切自然数n恒成立  ,即要loga(2x+1)≥0,讨论a的取值得到x的范围.
,即要loga(2x+1)≥0,讨论a的取值得到x的范围.解答:解:(1)由双曲线方程得:Cn=an+an+1,又因为一条渐近线
 .
.∴
 ,∴an=4•2n+1=2n+1
,∴an=4•2n+1=2n+1∴Cn=3•2n
(2)Sn=6(2n-1),Tn=8(22n-1),∴

(3)令S=
 +
+ +…+
+…+ =
= +
+ +…+
+…+
由错位相减得

故原不等式
 恒成立
恒成立∴loga(2x+1)≥0
(i)当a>1时,2x+1≥1⇒x≥0
(ii)当

∴

点评:本题以双曲线为载体,考查考查学生灵活运用等比数列的通项公式,以及掌握双曲线的简单性质,理解不等式恒成立时取到的条件,掌握对数函数的图象与性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知双曲线an-1y2-anx2=an-1an的焦点在y轴上,一条渐近线方程为y=
x,其中{an}是以4为首项的正数数列,则数列{an}的通项公式是( )
| 2 |
A、an=2
| ||
| B、an=21-n | ||
| C、an=4n-2 | ||
| D、an=2n+1 |
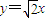 ,其中{an}是以4为首项的正数数列,则数列{an}的通项公式是( )
,其中{an}是以4为首项的正数数列,则数列{an}的通项公式是( )