题目内容
下列特称命题中假命题的个数是( )
(1)?x∈R,使2x2+x+1=0
(2)存在两条相交直线垂直于同一个平面
(3)?x∈R,x2≤0.
(1)?x∈R,使2x2+x+1=0
(2)存在两条相交直线垂直于同一个平面
(3)?x∈R,x2≤0.
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1)2x2+x+1=0中,△=12-4×2×1=-7<0,2x2+x+1=0无实数解,可判断(1);
(2)垂直于同一平面的两条直线平行,可判断(2);
(3))?x=0∈R,x2≤0,可判断(3).
(2)垂直于同一平面的两条直线平行,可判断(2);
(3))?x=0∈R,x2≤0,可判断(3).
解答:
解:(1)因为2x2+x+1=0中,△=12-4×2×1=-7<0,
所以,不?x∈R,使2x2+x+1=0,故(1)不正确;
(2)垂直于同一平面的两条直线平行,故不存在两条相交直线垂直于同一个平面,故(2)不正确;
(3)?x=0∈R,x2≤0,(3)正确.
故选:C.
所以,不?x∈R,使2x2+x+1=0,故(1)不正确;
(2)垂直于同一平面的两条直线平行,故不存在两条相交直线垂直于同一个平面,故(2)不正确;
(3)?x=0∈R,x2≤0,(3)正确.
故选:C.
点评:本题考查命题的真假判断与应用,考查面面垂直的性质与特称命题的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
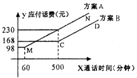 电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |
若数列{an}为等差数列,ap=q,aq=p(p≠q),则ap+q=( )
| A、p+q | ||
| B、0 | ||
| C、-(p+q) | ||
D、
|
在空间坐标中,O为坐标原点,A(1,2,3),则|OA|等于( )
A、
| ||
B、
| ||
C、2
| ||
D、
|
下列各式中,正确的是( )
A、2
| ||
B、2
| ||
C、{2
| ||
D、{2
|