题目内容
6.如图1,在矩形ABCD中,AB=5,AD=2,点E,F分别在边AB,CD上,且AE=4,DF=1,AC交DE于点G.现将△ADF沿AF折起,使得平面ADF⊥平面ABCF,得到图2.(Ⅰ)在图2中,求证:CE⊥DG;
(Ⅱ)若点M是线段DE上的一动点,问点M在什么位置时,二面角M-AF-D的余弦值为$\frac{3}{5}$.
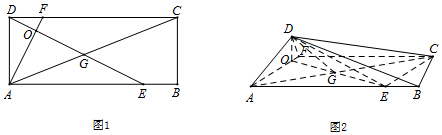
分析 (Ⅰ)推导出DE⊥AF,DO⊥OF,EO⊥AF,从而DO⊥平面ABCF,进而DO⊥CE,推导出四边形AECF为平行四边形,从而CE⊥OE,进而CE⊥平面DOE,由此能证明CE⊥DG.
(Ⅱ)以点O为原点建立平面直角坐标系,利用向量法能求出当点M在线段DE的四等分点且DM=$\frac{1}{4}$DE时,二面角M-AF-D的余弦值为$\frac{3}{5}$.
解答 证明:(Ⅰ)∵在矩形ABCD中,AB=5,AD=2,AE=4,DF=1,
∴tan$∠DAF=\frac{DF}{AD}=\frac{AD}{AE}$=tan∠AED,
∴∠AOE=90°,即DE⊥AF.
∴在图2中,DO⊥OF,EO⊥AF.
又∵平面ADF⊥平面ABCF,平面ADF∩平面ABCF=AF,
∴DO⊥平面ABCF,∴DO⊥CE,
依题意,AE∥CF,且AE=CF,∴四边形AECF为平行四边形.
∴CE∥AF,∴CE⊥OE,又∵OD∩OE=O,
∴CE⊥平面DOE,又∵DG?平面DOE,∴CE⊥DG.
解:(Ⅱ)如图1,在Rt△ADF中,AF=$\sqrt{5}$,OD=$\frac{2}{\sqrt{5}}$,OF=$\frac{1}{\sqrt{5}}$,
∵DF∥AE,AE=4DF,∴OE=4OD=$\frac{8}{\sqrt{5}}$.
如图,以点O为原点建立平面直角坐标系,
则A($\frac{4}{\sqrt{5}}$,0,0),F(-$\frac{1}{\sqrt{5}}$,0,0),D(0,0,$\frac{2}{\sqrt{5}}$),E(0,$\frac{8}{\sqrt{5}}$,0),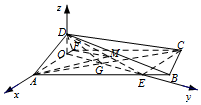
∴$\overrightarrow{FA}$=($\sqrt{5}$,0,0),$\overrightarrow{ED}$=(0,-$\frac{8}{\sqrt{5}}$,$\frac{2}{\sqrt{5}}$),$\overrightarrow{AE}$=(-$\frac{4}{\sqrt{5}}$,$\frac{8}{\sqrt{5}}$,0),
∵EO⊥AF,∴OE⊥平面ADF,
∴$\overrightarrow{n}$=(0,1,0)为平面ADF的法向量.
设$\overrightarrow{EM}=λ\overrightarrow{ED}$,则$\overrightarrow{AM}$=$\overrightarrow{AE}+λ\overrightarrow{ED}$=(-$\frac{4}{\sqrt{5}}$,$\frac{8}{\sqrt{5}}(1-λ)$,$\frac{2}{\sqrt{5}}λ$),
设$\overrightarrow{m}$=(x,y,z)为平面AFM的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{FA}=\sqrt{5}x=0}\\{\overrightarrow{m}•\overrightarrow{AM}=-\frac{4}{\sqrt{5}}x+\frac{8}{\sqrt{5}}(1-λ)y+\frac{2}{\sqrt{5}}λz=0}\end{array}\right.$,取y=λ,得$\overrightarrow{m}$=(0,λ,4(λ-1)),
∵二面角M-AF-D的余弦值为$\frac{3}{5}$,∴|cos<$\overrightarrow{m},\overrightarrow{n}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{|λ|}{\sqrt{{λ}^{2}+16(λ-1)^{2}}}$=$\frac{3}{5}$,
整理得8λ2-18λ+9=0,解得λ=$\frac{3}{4}$或λ=$\frac{3}{2}$(舍),
∴当点M在线段DE的四等分点且DM=$\frac{1}{4}$DE时,二面角M-AF-D的余弦值为$\frac{3}{5}$.
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法及应用,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4 |
| A. | $0<\frac{a}{b}<1$ | B. | $ln\frac{a}{b}>0$ | C. | ca>cb | D. | ac-bc<0 |
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\sqrt{5}$ | D. | $\frac{5}{2}$ |
| A. | 4 | B. | 4i | C. | -4 | D. | -4i |
| A. | (0,2] | B. | [0,2] | C. | ∅ | D. | [1,2] |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |