题目内容
在数列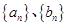 中,
中,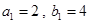 ,且
,且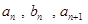 成等差数列,
成等差数列,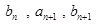 成等比数列
成等比数列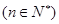 .
.
(1)求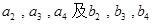 ;
;
(2)根据计算结果,猜想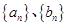 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
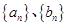 中,
中,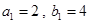 ,且
,且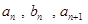 成等差数列,
成等差数列,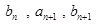 成等比数列
成等比数列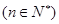 .
.(1)求
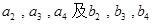 ;
;(2)根据计算结果,猜想
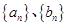 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.(1)  ,
, ;(2)
;(2)  ,证明过程见试题解析.
,证明过程见试题解析.
 ,
, ;(2)
;(2)  ,证明过程见试题解析.
,证明过程见试题解析.试题分析:(1)由已知得
 ,令
,令 得
得 ,可得
,可得 ,又
,又 ,令
,令 得
得 ,可得
,可得 ,依次分别求得其余各项; (2)由(1)中结果,易猜想出
,依次分别求得其余各项; (2)由(1)中结果,易猜想出 ,用数学归纳法证明中,当
,用数学归纳法证明中,当 时,需证
时,需证 ,
, 方可得结论成立.
方可得结论成立.解:(1)由已知条件得
 ,
,由此算出
 ,
, .
.(2)由(1)的计算可以猜想
 ,
, 下面用数学归纳法证明:
①当
 时,由已知
时,由已知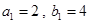 可得结论成立,
可得结论成立,②假设当

 时猜想成立,即
时猜想成立,即 .
.那么,当
 时,
时,  ,
, ,
,因此当
 时,结论也成立.
时,结论也成立.当①和②知,对一切
 ,都有
,都有 成立. 12分
成立. 12分
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
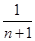 +
+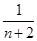 +…+
+…+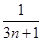 >
>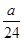 对一切正整数n都成立,猜想正整数a的最大值,并证明结论.
对一切正整数n都成立,猜想正整数a的最大值,并证明结论.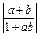 <1.
<1.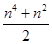 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )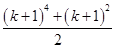
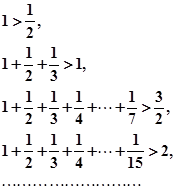
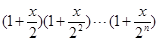 的展开式中,
的展开式中,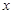 的系数为
的系数为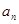 ,
,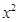 的系数为
的系数为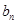 ,其中
,其中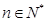
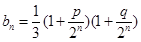 ,对
,对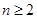 恒成立?证明你的结论.
恒成立?证明你的结论. ,考查
,考查 ;
; ;
; .
. 都成立的类似不等式,并用数学归纳法加以证明.
都成立的类似不等式,并用数学归纳法加以证明.