题目内容
若不等式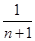 +
+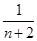 +…+
+…+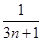 >
>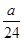 对一切正整数n都成立,猜想正整数a的最大值,并证明结论.
对一切正整数n都成立,猜想正整数a的最大值,并证明结论.
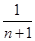 +
+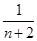 +…+
+…+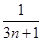 >
>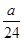 对一切正整数n都成立,猜想正整数a的最大值,并证明结论.
对一切正整数n都成立,猜想正整数a的最大值,并证明结论.见解析
解:当n=1时,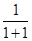 +
+ +
+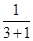 >
>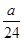 ,
,
即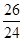 >
>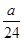 ,所以a<26,而a是正整数,
,所以a<26,而a是正整数,
所以取a=25.
下面用数学归纳法证明:
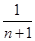 +
+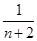 +…+
+…+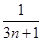 >
>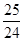 .
.
①当n=1时,已证;
②假设当n=k时,不等式成立,
即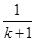 +
+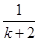 +…+
+…+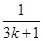 >
>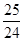 .
.
则当n=k+1时,有
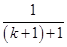 +
+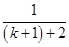 +…+
+…+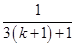
=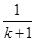 +
+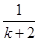 +…+
+…+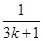 +
+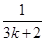 +
+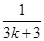 +
+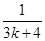 -
-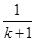 >
>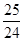 +[
+[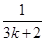 +
+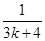 -
-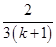 ].
].
因为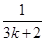 +
+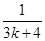 =
= >
>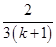 ,
,
所以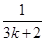 +
+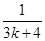 -
-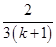 >0,
>0,
所以当n=k+1时,不等式也成立.
由①②知,对一切正整数n,
都有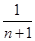 +
+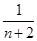 +…+
+…+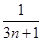 >
>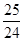 ,
,
所以a的最大值等于25.
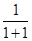 +
+ +
+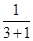 >
>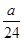 ,
,即
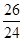 >
>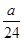 ,所以a<26,而a是正整数,
,所以a<26,而a是正整数,所以取a=25.
下面用数学归纳法证明:
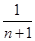 +
+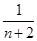 +…+
+…+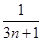 >
>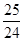 .
.①当n=1时,已证;
②假设当n=k时,不等式成立,
即
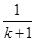 +
+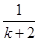 +…+
+…+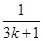 >
>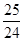 .
.则当n=k+1时,有
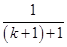 +
+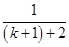 +…+
+…+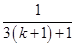
=
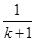 +
+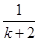 +…+
+…+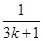 +
+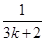 +
+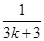 +
+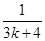 -
-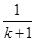 >
>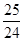 +[
+[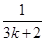 +
+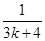 -
-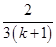 ].
].因为
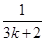 +
+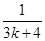 =
= >
>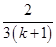 ,
,所以
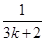 +
+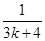 -
-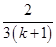 >0,
>0,所以当n=k+1时,不等式也成立.
由①②知,对一切正整数n,
都有
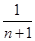 +
+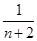 +…+
+…+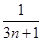 >
>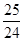 ,
,所以a的最大值等于25.

练习册系列答案
相关题目
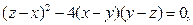 求证:
求证: 成等差数列。
成等差数列。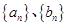 中,
中,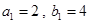 ,且
,且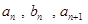 成等差数列,
成等差数列,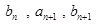 成等比数列
成等比数列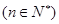 .
.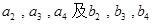 ;
;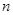 个图包含______个互不重叠的单位正方形。
个图包含______个互不重叠的单位正方形。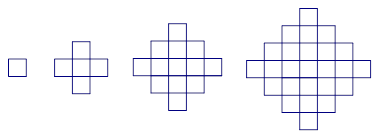
 (
( )时,从“n=
)时,从“n= ”到“n=
”到“n= ”的证明,左边需增添的代数式是___________.
”的证明,左边需增添的代数式是___________. 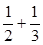 +…+
+…+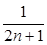 (n∈N*)中,当n=1时式子值为1+
(n∈N*)中,当n=1时式子值为1+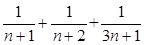 (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+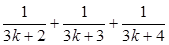
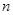 条两两相交的弦,把圆最多分成 部分.
条两两相交的弦,把圆最多分成 部分.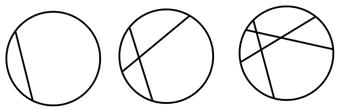
 +
+ +…+
+…+ >
> 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.