题目内容
由下列各个不等式:
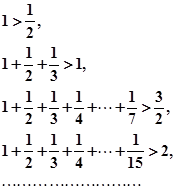
你能得到一个怎样的一般不等式?并加以证明.
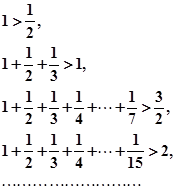
你能得到一个怎样的一般不等式?并加以证明.

试题分析:根据给出的式子的规律总结出能得到的不等式的通式
 证明则需要运用数学归纳法.
证明则需要运用数学归纳法.根据给出的几个不等式可以猜想第
 个不等式,即一般不等式为:
个不等式,即一般不等式为:
用数学归纳法证明如下:
(1)当n="1" 时
 ,猜想成立.
,猜想成立.(2)假设当时
 猜想成立,即
猜想成立,即
则当
 时,
时,








这就说明
 猜想也成立,由(1)(2)知,猜想对一切
猜想也成立,由(1)(2)知,猜想对一切 都成立.
都成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
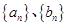 中,
中,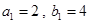 ,且
,且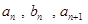 成等差数列,
成等差数列,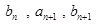 成等比数列
成等比数列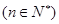 .
.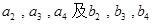 ;
;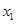 ,
,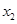 是函数
是函数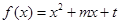 的两个零点,其中常数
的两个零点,其中常数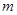 ,
,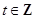 ,设
,设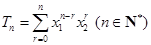 .
.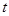 表示
表示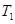 ,
,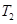 ;
;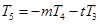 ;
;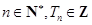 .
. ≥
≥ .
.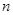 个图包含______个互不重叠的单位正方形。
个图包含______个互不重叠的单位正方形。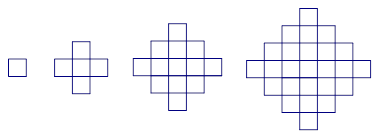
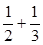 +…+
+…+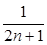 (n∈N*)中,当n=1时式子值为1+
(n∈N*)中,当n=1时式子值为1+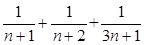 (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+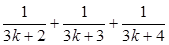
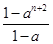 (n∈N*,a≠1),在验证n=1时,左边所得的项为( )
(n∈N*,a≠1),在验证n=1时,左边所得的项为( ) +
+ +…+
+…+ >
> 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.