题目内容
如图所示，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB＝90°，BD交AC于E，AB＝2.
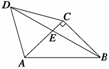
(1)求cos∠CBE的值；
(2)求AE.
解 (1)∵∠BCD＝90°＋60°＝150°，CB＝AC＝CD，
∴∠CBE＝15°.
∴cos∠CBE＝cos(45°－30°)＝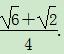
(2)在△ABE中，AB＝2，
由正弦定理得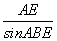
＝
，
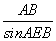即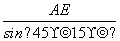
＝
，
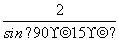故AE＝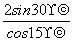
＝
＝
－
.
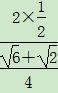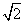练习册系列答案
相关题目
题目内容
如图所示，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB＝90°，BD交AC于E，AB＝2.
(1)求cos∠CBE的值；
(2)求AE.
解 (1)∵∠BCD＝90°＋60°＝150°，CB＝AC＝CD，
∴∠CBE＝15°.
∴cos∠CBE＝cos(45°－30°)＝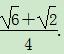
(2)在△ABE中，AB＝2，
由正弦定理得＝，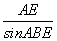
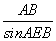即＝，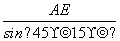
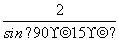故AE＝＝＝－.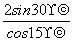
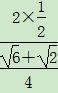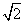sin ωx)，n＝(f(x)，cos ωx)，其中ω>0，且m⊥n，又函数f(x)的图象任意两相邻对称轴的间距为
.
的值．
D．4＋2
，AC＝1，则△ABC的面积是( )
B.
的图像如下列图中，经过原点和（1,1），且对任意
,由关系式
得到数列{
}，满足
，则该函数的图像为（ ）